


Next: Electromagnetic Radiation
Up: Time-Dependent Perturbation Theory
Previous: Perturbation Expansion
Consider a (Hermitian) perturbation which oscillates sinusoidally
in time. This is usually termed a harmonic perturbation. Such
a perturbation takes the form
 |
(1067) |
where 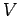 is, in general, a function of position, momentum, and spin operators.
is, in general, a function of position, momentum, and spin operators.
It follows from Eqs. (1064) and (1067) that, to first-order,
![\begin{displaymath}
c_f(t) = - \frac{\rm i}{\hbar}\int_0^t\left[V_{fi} \exp( {...
... i} \omega t')\right]
\exp( {\rm i} \omega_{fi} t') dt',
\end{displaymath}](img2482.png) |
(1068) |
where
Integration with respect to 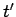 yields
yields
where
 |
(1072) |
Figure 25:
The functions  (dashed curve) and
(dashed curve) and
 (solid curve). The vertical dotted lines denote
the region
(solid curve). The vertical dotted lines denote
the region 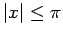 .
.
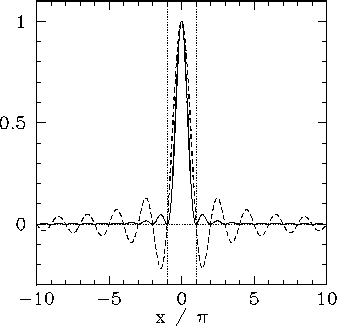 |
Now, the function 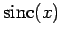 takes its largest values when
takes its largest values when
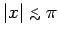 , and is fairly negligible when
, and is fairly negligible when 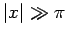 (see Fig. 25). Thus, the first and second terms
on the right-hand side of Eq. (1071) are only
non-negligible when
(see Fig. 25). Thus, the first and second terms
on the right-hand side of Eq. (1071) are only
non-negligible when
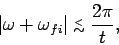 |
(1073) |
and
 |
(1074) |
respectively.
Clearly, as  increases, the ranges in
increases, the ranges in 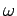 over which these two
terms are non-negligible gradually shrink in size.
Eventually, when
over which these two
terms are non-negligible gradually shrink in size.
Eventually, when
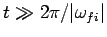 , these two ranges become strongly non-overlapping.
Hence, in this limit,
, these two ranges become strongly non-overlapping.
Hence, in this limit,
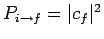 yields
yields
![\begin{displaymath}
P_{i\rightarrow f}(t) = \frac{t^2}{\hbar^2}\left\{
\vert V_{...
...} {\rm sinc}^2\left[(\omega-\omega_{fi}) t/2\right]\right\}.
\end{displaymath}](img2501.png) |
(1075) |
Now, the function
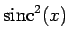 is very strongly peaked at
is very strongly peaked at  ,
and is completely negligible for
,
and is completely negligible for
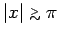 (see Fig. 25). It follows that the above expression exhibits a
resonant response to the applied perturbation at the frequencies
(see Fig. 25). It follows that the above expression exhibits a
resonant response to the applied perturbation at the frequencies
 . Moreover,
the widths of these resonances decease linearly as time increases. At each
of the resonances (i.e., at
. Moreover,
the widths of these resonances decease linearly as time increases. At each
of the resonances (i.e., at
 ), the transition
probability
), the transition
probability
 varies as
varies as 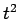 [since
[since
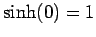 ]. This behaviour
is entirely consistent with our earlier result (1044), for the two-state
system, in the limit
]. This behaviour
is entirely consistent with our earlier result (1044), for the two-state
system, in the limit
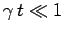 (recall that our perturbative
solution is only valid as long as
(recall that our perturbative
solution is only valid as long as
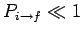 ).
).
The resonance at
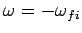 corresponds to
corresponds to
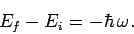 |
(1076) |
This implies that the system loses energy 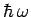 to the
perturbing field, whilst making a transition to a final state whose
energy is less than the initial state by
to the
perturbing field, whilst making a transition to a final state whose
energy is less than the initial state by 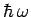 . This process is
known as stimulated emission. The resonance at
. This process is
known as stimulated emission. The resonance at
 corresponds to
corresponds to
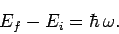 |
(1077) |
This implies that the system gains energy 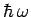 from the
perturbing field, whilst making a transition to a final state whose
energy is greater than that of the initial state by
from the
perturbing field, whilst making a transition to a final state whose
energy is greater than that of the initial state by 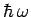 . This
process is known as absorption.
. This
process is known as absorption.
Stimulated emission and absorption are mutually exclusive processes, since the
first requires 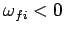 , whereas the second requires
, whereas the second requires 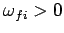 . Hence, we can write the transition probabilities for
both processes separately. Thus, from (1075), the
transition probability for stimulated emission is
. Hence, we can write the transition probabilities for
both processes separately. Thus, from (1075), the
transition probability for stimulated emission is
![\begin{displaymath}
P_{i\rightarrow f}^{stm}(t) = \frac{t^2}{\hbar^2}
\vert V_...
...ert^{ 2} {\rm sinc}^2\left[(\omega-\omega_{if}) t/2\right],
\end{displaymath}](img2515.png) |
(1078) |
where we have made use of the facts that
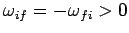 ,
and
,
and
 . Likewise, the transition probability
for absorption is
. Likewise, the transition probability
for absorption is
![\begin{displaymath}
P_{i\rightarrow f}^{abs}(t) = \frac{t^2}{\hbar^2}
\vert V_...
...ert^{ 2} {\rm sinc}^2\left[(\omega-\omega_{fi}) t/2\right].
\end{displaymath}](img2518.png) |
(1079) |



Next: Electromagnetic Radiation
Up: Time-Dependent Perturbation Theory
Previous: Perturbation Expansion
Richard Fitzpatrick
2010-07-20

![]() takes its largest values when
takes its largest values when
![]() , and is fairly negligible when
, and is fairly negligible when ![]() (see Fig. 25). Thus, the first and second terms
on the right-hand side of Eq. (1071) are only
non-negligible when
(see Fig. 25). Thus, the first and second terms
on the right-hand side of Eq. (1071) are only
non-negligible when
![]() is very strongly peaked at
is very strongly peaked at ![]() ,
and is completely negligible for
,
and is completely negligible for
![]() (see Fig. 25). It follows that the above expression exhibits a
resonant response to the applied perturbation at the frequencies
(see Fig. 25). It follows that the above expression exhibits a
resonant response to the applied perturbation at the frequencies
![]() . Moreover,
the widths of these resonances decease linearly as time increases. At each
of the resonances (i.e., at
. Moreover,
the widths of these resonances decease linearly as time increases. At each
of the resonances (i.e., at
![]() ), the transition
probability
), the transition
probability
![]() varies as
varies as ![]() [since
[since
![]() ]. This behaviour
is entirely consistent with our earlier result (1044), for the two-state
system, in the limit
]. This behaviour
is entirely consistent with our earlier result (1044), for the two-state
system, in the limit
![]() (recall that our perturbative
solution is only valid as long as
(recall that our perturbative
solution is only valid as long as
![]() ).
).
![]() corresponds to
corresponds to
![]() , whereas the second requires
, whereas the second requires ![]() . Hence, we can write the transition probabilities for
both processes separately. Thus, from (1075), the
transition probability for stimulated emission is
. Hence, we can write the transition probabilities for
both processes separately. Thus, from (1075), the
transition probability for stimulated emission is