


Next: Spin Magnetic Resonance
Up: Time-Dependent Perturbation Theory
Previous: Preliminary Analysis
Consider a system in which the time-independent Hamiltonian possesses
two eigenstates, denoted
Suppose, for the sake of simplicity, that the diagonal elements of
the interaction Hamiltonian, 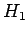 , are zero: i.e.,
, are zero: i.e.,
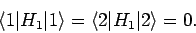 |
(1033) |
The off-diagonal elements are assumed to oscillate sinusoidally
at some frequency 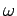 : i.e.,
: i.e.,
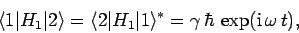 |
(1034) |
where 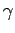 and
and 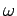 are real. Note that it is only the off-diagonal
matrix elements which give rise to the effect which we are interested
in--namely, transitions between states 1 and 2.
are real. Note that it is only the off-diagonal
matrix elements which give rise to the effect which we are interested
in--namely, transitions between states 1 and 2.
For a two-state system, Eq. (1028) reduces to
where
 . The above two equations can be combined to give a second-order
differential equation for the time-variation of the amplitude
. The above two equations can be combined to give a second-order
differential equation for the time-variation of the amplitude 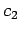 : i.e.,
: i.e.,
 |
(1037) |
Once we have solved for 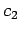 , we can use Eq. (1036)
to obtain the amplitude
, we can use Eq. (1036)
to obtain the amplitude  . Let us search for a solution
in which the system is certain to be in state 1 (and, thus, has
no chance of being in state 2) at time
. Let us search for a solution
in which the system is certain to be in state 1 (and, thus, has
no chance of being in state 2) at time  .
Thus, our initial conditions are
.
Thus, our initial conditions are 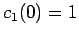 and
and 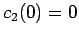 .
It is easily demonstrated that the appropriate solutions to (1037) and
(1036) are
.
It is easily demonstrated that the appropriate solutions to (1037) and
(1036) are
where
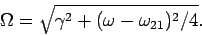 |
(1040) |
Now, the probability of finding the system in state 1 at time  is
simply
is
simply
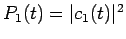 . Likewise, the probability of finding the system
in state 2 at time
. Likewise, the probability of finding the system
in state 2 at time  is
is
 . It follows that
. It follows that
This result is known as Rabi's formula.
Equation (1042) exhibits all the features of a classic resonance.
At resonance, when the oscillation frequency of the perturbation, 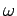 ,
matches the frequency
,
matches the frequency 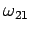 , we find that
, we find that
According to the above result, the system starts off
in state 1 at  . After a time interval
. After a time interval
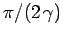 it is certain to be
in state 2. After a further time interval
it is certain to be
in state 2. After a further time interval
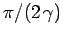 it is certain
to be in state 1 again, and so on. Thus, the system periodically
flip-flops between states 1 and 2 under the influence of the time-dependent
perturbation. This implies that the system alternatively absorbs and emits
energy from the source of the perturbation.
it is certain
to be in state 1 again, and so on. Thus, the system periodically
flip-flops between states 1 and 2 under the influence of the time-dependent
perturbation. This implies that the system alternatively absorbs and emits
energy from the source of the perturbation.
The absorption-emission cycle also takes place away from the resonance,
when
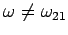 . However, the amplitude of the
oscillation in the coefficient
. However, the amplitude of the
oscillation in the coefficient 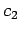 is reduced. This means that the maximum
value of
is reduced. This means that the maximum
value of 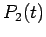 is no longer unity, nor is the minimum of
is no longer unity, nor is the minimum of 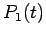 zero. In fact, if we plot the maximum value of
zero. In fact, if we plot the maximum value of 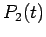 as a function
of the applied frequency,
as a function
of the applied frequency, 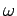 , we obtain a resonance curve whose
maximum (unity) lies at the resonance, and whose full-width half-maximum
(in frequency) is
, we obtain a resonance curve whose
maximum (unity) lies at the resonance, and whose full-width half-maximum
(in frequency) is 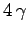 . Thus, if the applied frequency differs
from the resonant frequency by substantially more than
. Thus, if the applied frequency differs
from the resonant frequency by substantially more than 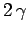 then the probability of the system jumping from state 1 to state 2 is
always very small. In other words, the time-dependent
perturbation is only effective at causing transitions between states 1 and 2
if its frequency of oscillation lies in the approximate
range
then the probability of the system jumping from state 1 to state 2 is
always very small. In other words, the time-dependent
perturbation is only effective at causing transitions between states 1 and 2
if its frequency of oscillation lies in the approximate
range
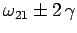 . Clearly, the weaker
the perturbation (i.e., the smaller
. Clearly, the weaker
the perturbation (i.e., the smaller 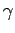 becomes), the narrower
the resonance.
becomes), the narrower
the resonance.



Next: Spin Magnetic Resonance
Up: Time-Dependent Perturbation Theory
Previous: Preliminary Analysis
Richard Fitzpatrick
2010-07-20
![$\displaystyle \left(\frac{-{\rm i} \gamma}{\Omega}\right)\exp\!\left[\frac{-{\rm i} (\omega-\omega_{21}) t}{2}\right]\sin(\Omega t),$](img2422.png)
![$\displaystyle \exp\!\left[\frac{{\rm i} (\omega-\omega_{21}) t}{2}\right]
\cos(\Omega t)$](img2424.png)
![$\displaystyle - \left[\frac{{\rm i} (\omega-\omega_{21})}{2 \Omega} \right]\exp\!\left[\frac{{\rm i} (\omega-\omega_{21}) t}{2}\right]\sin(\Omega t),$](img2425.png)
![]() is
simply
is
simply
![]() . Likewise, the probability of finding the system
in state 2 at time
. Likewise, the probability of finding the system
in state 2 at time ![]() is
is
![]() . It follows that
. It follows that
![]() ,
matches the frequency
,
matches the frequency ![]() , we find that
, we find that
![]() . However, the amplitude of the
oscillation in the coefficient
. However, the amplitude of the
oscillation in the coefficient ![]() is reduced. This means that the maximum
value of
is reduced. This means that the maximum
value of ![]() is no longer unity, nor is the minimum of
is no longer unity, nor is the minimum of ![]() zero. In fact, if we plot the maximum value of
zero. In fact, if we plot the maximum value of ![]() as a function
of the applied frequency,
as a function
of the applied frequency, ![]() , we obtain a resonance curve whose
maximum (unity) lies at the resonance, and whose full-width half-maximum
(in frequency) is
, we obtain a resonance curve whose
maximum (unity) lies at the resonance, and whose full-width half-maximum
(in frequency) is ![]() . Thus, if the applied frequency differs
from the resonant frequency by substantially more than
. Thus, if the applied frequency differs
from the resonant frequency by substantially more than ![]() then the probability of the system jumping from state 1 to state 2 is
always very small. In other words, the time-dependent
perturbation is only effective at causing transitions between states 1 and 2
if its frequency of oscillation lies in the approximate
range
then the probability of the system jumping from state 1 to state 2 is
always very small. In other words, the time-dependent
perturbation is only effective at causing transitions between states 1 and 2
if its frequency of oscillation lies in the approximate
range
![]() . Clearly, the weaker
the perturbation (i.e., the smaller
. Clearly, the weaker
the perturbation (i.e., the smaller ![]() becomes), the narrower
the resonance.
becomes), the narrower
the resonance.