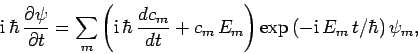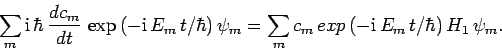Next: Two-State System
Up: Time-Dependent Perturbation Theory
Previous: Introduction
Preliminary Analysis
Suppose that at 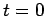 the state of the system is represented by
the state of the system is represented by
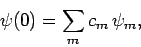 |
(1019) |
where the 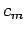 are complex numbers. Thus, the initial state is some
linear superposition of the unperturbed energy eigenstates. In the
absence of the time-dependent perturbation, the time evolution
of the system is simply (see Sect. 4.12)
are complex numbers. Thus, the initial state is some
linear superposition of the unperturbed energy eigenstates. In the
absence of the time-dependent perturbation, the time evolution
of the system is simply (see Sect. 4.12)
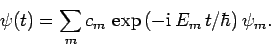 |
(1020) |
Now, the probability of finding the system in state  at time
at time  is
is
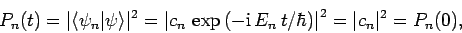 |
(1021) |
since the unperturbed eigenstates are assummed to be orthonormal:
i.e.,
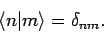 |
(1022) |
Clearly, with  , the probability of finding the system in state
, the probability of finding the system in state
 at time
at time 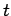 is exactly the same as the probability of finding the
system in this state at the initial time,
is exactly the same as the probability of finding the
system in this state at the initial time, 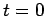 . However, with
. However, with 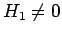 ,
we expect
,
we expect 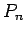 --and, hence,
--and, hence, 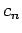 --to vary with time. Thus, we can write
--to vary with time. Thus, we can write
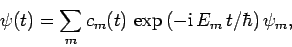 |
(1023) |
where
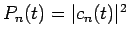 . Here, we have carefully separated the
fast phase oscillation of the eigenstates, which depends on the
unperturbed Hamiltonian, from the slow variation of the
amplitudes
. Here, we have carefully separated the
fast phase oscillation of the eigenstates, which depends on the
unperturbed Hamiltonian, from the slow variation of the
amplitudes 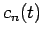 , which depends entirely on the perturbation
(i.e.,
, which depends entirely on the perturbation
(i.e., 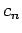 is constant in time if
is constant in time if 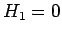 ). Note that in Eq. (1023) the eigenstates
). Note that in Eq. (1023) the eigenstates 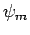 are time-independent (they are actually the eigenstates of
are time-independent (they are actually the eigenstates of 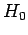 evaluated at the initial time,
evaluated at the initial time, 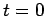 ).
).
The time-dependent Schrödinger equation [see Eq. (199)]
yields
![\begin{displaymath}
{\rm i} \hbar \frac{\partial\psi(t)}{\partial t} = H(t) \psi(t)
= [H_0+H_1(t)] \psi(t).
\end{displaymath}](img2402.png) |
(1024) |
Now, it follows from Eq. (1023) that
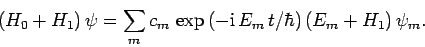 |
(1025) |
We also have
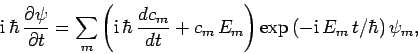 |
(1026) |
since the 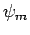 are time-independent. According to
Eq. (1024), we can equate the right-hand sides of the previous
two equations to obtain
are time-independent. According to
Eq. (1024), we can equate the right-hand sides of the previous
two equations to obtain
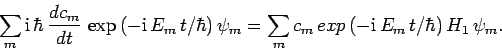 |
(1027) |
Projecting out the component of the above equation which is proportional
to 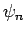 , using Eq. (1022), we obtain
, using Eq. (1022), we obtain
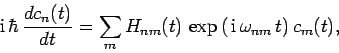 |
(1028) |
where
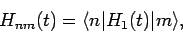 |
(1029) |
and
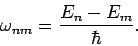 |
(1030) |
Suppose that there are 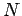 linearly independent eigenstates of
the unperturbed Hamiltonian. According to Eqs. (1028),
the time-dependence of the set of
linearly independent eigenstates of
the unperturbed Hamiltonian. According to Eqs. (1028),
the time-dependence of the set of 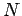 coefficients
coefficients 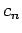 , which specify the
probabilities of finding the system in these eigenstates at time
, which specify the
probabilities of finding the system in these eigenstates at time 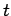 , is determined
by
, is determined
by 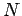 coupled first-order differential equations. Note that Eqs. (1028)
are exact--we have made no approximations at this stage. Unfortunately,
we cannot generally find exact solutions to these equations. Instead, we
have to obtain approximate solutions via suitable
expansions in small quantities. However, for the particuilarly
simple case of a two-state system (i.e.,
coupled first-order differential equations. Note that Eqs. (1028)
are exact--we have made no approximations at this stage. Unfortunately,
we cannot generally find exact solutions to these equations. Instead, we
have to obtain approximate solutions via suitable
expansions in small quantities. However, for the particuilarly
simple case of a two-state system (i.e., 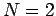 ), it is actually
possible to solve Eqs. (1028) without approximation. This solution
is of great practical importance.
), it is actually
possible to solve Eqs. (1028) without approximation. This solution
is of great practical importance.



Next: Two-State System
Up: Time-Dependent Perturbation Theory
Previous: Introduction
Richard Fitzpatrick
2010-07-20