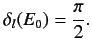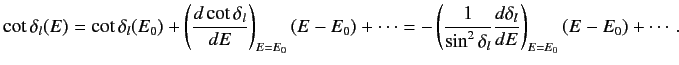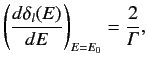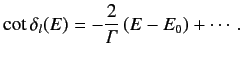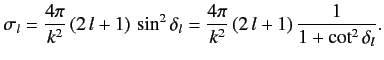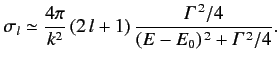Next: Exercises
Up: Scattering Theory
Previous: Low Energy Scattering
There is a significant exception to the independence of the cross-section on energy. Suppose that the quantity
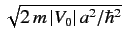 is slightly less than
is slightly less than 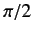 . As the incident energy increases,
. As the incident energy increases, 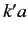 ,
which is given by Equation (1018), can reach the value
,
which is given by Equation (1018), can reach the value 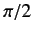 . In this case,
. In this case,
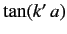 becomes infinite, so we can no longer assume that the right-hand side of Equation (1013) is small. In fact,
at the value of the incident energy
when
becomes infinite, so we can no longer assume that the right-hand side of Equation (1013) is small. In fact,
at the value of the incident energy
when
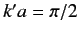 , it follows from Equation (1013) that
, it follows from Equation (1013) that
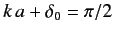 ,
or
,
or
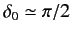 (because we are assuming that
(because we are assuming that 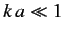 ).
This implies that
).
This implies that
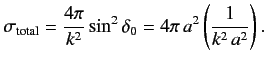 |
(1020) |
Note that the cross-section now depends on the energy. Furthermore, the
magnitude of the cross-section is much larger than that given in Equation (1017)
for
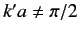 (since
(since 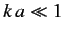 ).
).
The origin of this rather strange behaviour is quite simple. The condition
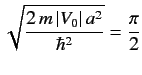 |
(1021) |
is equivalent to the condition that a spherical well of depth
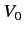 possesses a bound state at zero energy. Thus, for a potential
well that satisfies the above equation, the energy of the scattering system
is essentially the same as the energy of the bound state. In this situation,
an incident particle would like to form a bound state in the potential
well. However, the bound state is not stable, because the system has a small
positive energy. Nevertheless, this sort of resonance scattering
is best understood as the capture of an incident particle to form
a metastable bound state, and the subsequent decay of the bound state
and release of the particle. The cross-section for resonance scattering
is generally far higher than that for non-resonance scattering.
possesses a bound state at zero energy. Thus, for a potential
well that satisfies the above equation, the energy of the scattering system
is essentially the same as the energy of the bound state. In this situation,
an incident particle would like to form a bound state in the potential
well. However, the bound state is not stable, because the system has a small
positive energy. Nevertheless, this sort of resonance scattering
is best understood as the capture of an incident particle to form
a metastable bound state, and the subsequent decay of the bound state
and release of the particle. The cross-section for resonance scattering
is generally far higher than that for non-resonance scattering.
We have seen that there is a resonant effect when the phase-shift of
the 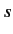 -wave takes the value
-wave takes the value 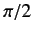 . There is nothing special about
the
. There is nothing special about
the 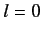 partial wave, so it is reasonable to assume that there
is a similar resonance when the phase-shift of the
partial wave, so it is reasonable to assume that there
is a similar resonance when the phase-shift of the 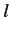 th partial
wave is
th partial
wave is 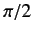 . Suppose that
. Suppose that 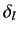 attains the value
attains the value
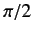 at the incident energy
at the incident energy 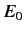 , so that
, so that
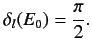 |
(1022) |
Let us expand
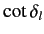 in the vicinity of the resonant energy:
in the vicinity of the resonant energy:
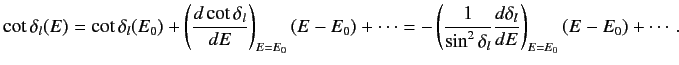 |
(1023) |
Defining
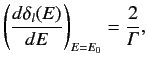 |
(1024) |
we obtain
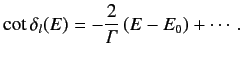 |
(1025) |
Recall, from Equation (984), that the contribution of the 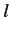 th partial wave
to the scattering cross-section is
th partial wave
to the scattering cross-section is
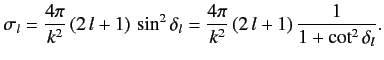 |
(1026) |
Thus,
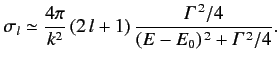 |
(1027) |
This is the famous Breit-Wigner formula. The variation of
the partial cross-section 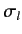 with the incident energy has
the form of a classical resonance curve. The quantity
with the incident energy has
the form of a classical resonance curve. The quantity
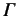 is
the width of the resonance (in energy). We can interpret the
Breit-Wigner formula as describing the absorption of an incident particle
to form a metastable state, of energy
is
the width of the resonance (in energy). We can interpret the
Breit-Wigner formula as describing the absorption of an incident particle
to form a metastable state, of energy 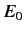 , and lifetime
, and lifetime
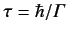 .
.



Next: Exercises
Up: Scattering Theory
Previous: Low Energy Scattering
Richard Fitzpatrick
2013-04-08
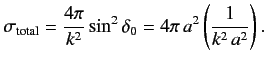
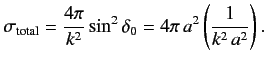
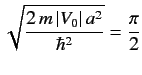
![]() -wave takes the value
-wave takes the value ![]() . There is nothing special about
the
. There is nothing special about
the ![]() partial wave, so it is reasonable to assume that there
is a similar resonance when the phase-shift of the
partial wave, so it is reasonable to assume that there
is a similar resonance when the phase-shift of the ![]() th partial
wave is
th partial
wave is ![]() . Suppose that
. Suppose that ![]() attains the value
attains the value
![]() at the incident energy
at the incident energy ![]() , so that
, so that