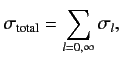Next: Determination of Phase-Shifts
Up: Scattering Theory
Previous: Partial Waves
The differential scattering cross-section
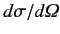 is simply
the modulus squared of the scattering amplitude
is simply
the modulus squared of the scattering amplitude 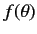 . The
total cross-section is given by
. The
total cross-section is given by
where
 . It follows that
. It follows that
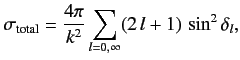 |
(981) |
where use has been made of Equation (967). A comparison of this result with
Equation (979) yields
![$\displaystyle \sigma_{\rm total} = \frac{4\pi}{k}\, {\rm Im}\left[f(0)\right],$](img2259.png) |
(982) |
since
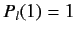 . This result is known as the optical theorem.
It is a reflection of the fact that the very existence of scattering
requires scattering in the forward (
. This result is known as the optical theorem.
It is a reflection of the fact that the very existence of scattering
requires scattering in the forward (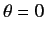 ) direction
in order to interfere with the incident wave, and thereby reduce the
probability current in this direction.
) direction
in order to interfere with the incident wave, and thereby reduce the
probability current in this direction.
It is usual to write
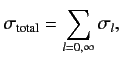 |
(983) |
where
 |
(984) |
is the  th partial cross-section: i.e., the contribution to the
total cross-section from the
th partial cross-section: i.e., the contribution to the
total cross-section from the  th partial wave. Note that the maximum
value for the
th partial wave. Note that the maximum
value for the  th partial cross-section occurs when the phase-shift
th partial cross-section occurs when the phase-shift 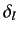 takes the value
takes the value 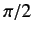 .
.



Next: Determination of Phase-Shifts
Up: Scattering Theory
Previous: Partial Waves
Richard Fitzpatrick
2013-04-08
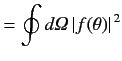
![$\displaystyle = \frac{1}{k^2} \oint d\varphi \int_{-1}^{1} d\mu \sum_l \sum_{l'...
...elta_l-\delta_{l'})]\, \sin\delta_l \,\sin\delta_{l'}\, P_l(\mu)\, P_{l'}(\mu),$](img2256.png)
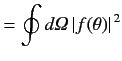
![$\displaystyle = \frac{1}{k^2} \oint d\varphi \int_{-1}^{1} d\mu \sum_l \sum_{l'...
...elta_l-\delta_{l'})]\, \sin\delta_l \,\sin\delta_{l'}\, P_l(\mu)\, P_{l'}(\mu),$](img2256.png)
![$\displaystyle \sigma_{\rm total} = \frac{4\pi}{k}\, {\rm Im}\left[f(0)\right],$](img2259.png)