


Next: Identical Particles
Up: Scattering Theory
Previous: Resonance Scattering
- Consider a scattering potential of the form
Calculate the differential scattering cross-section,
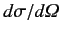 , using the Born approximation.
, using the Born approximation.
- Consider a scattering potential that takes the constant value
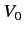 for
for 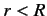 , and is zero
for
, and is zero
for 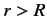 , where
, where 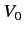 may be either positive or negative. Using the method of partial waves, show
that for
may be either positive or negative. Using the method of partial waves, show
that for
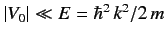 , and
, and 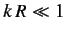 , the differential cross-section is isotropic, and that
the total cross-section is
, the differential cross-section is isotropic, and that
the total cross-section is
Suppose that the energy is slightly raised. Show that the angular distribution can then
be written in the form
Obtain an approximate expression for 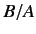 .
.
- Consider scattering by a repulsive
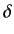 -shell potential:
-shell potential:
where 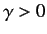 .
Find the equation that determines the
.
Find the equation that determines the 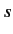 -wave phase-shift,
-wave phase-shift, 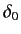 , as a function of
, as a function of 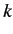 (where
(where
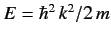 ).
Assume that
).
Assume that
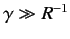 ,
, 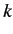 . Show that if
. Show that if
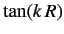 is not close to zero then the
is not close to zero then the 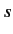 -wave phase-shift
resembles the hard sphere result discussed in the text. Furthermore, show that if
-wave phase-shift
resembles the hard sphere result discussed in the text. Furthermore, show that if
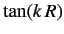 is close to zero then resonance
behavior is possible: i.e.,
is close to zero then resonance
behavior is possible: i.e.,
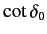 goes through zero from the positive side as
goes through zero from the positive side as 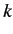 increases. Determine the
approximate positions of the resonances (retaining terms up to order
increases. Determine the
approximate positions of the resonances (retaining terms up to order 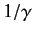 ). Compare the resonant
energies with the bound state energies for a particle confined within an infinite spherical well of radius
). Compare the resonant
energies with the bound state energies for a particle confined within an infinite spherical well of radius 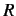 .
Obtain an approximate expression for the resonance width
.
Obtain an approximate expression for the resonance width
Show that the resonances become extremely sharp as
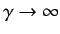 .
.
- Show that the differential cross-section for the elastic scattering of a fast electron by the ground-state of a hydrogen
atom is
where
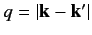 , and
, and 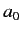 is the Bohr radius.
is the Bohr radius.



Next: Identical Particles
Up: Scattering Theory
Previous: Resonance Scattering
Richard Fitzpatrick
2013-04-08
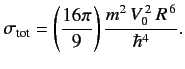
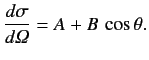
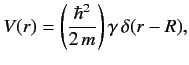
![$\displaystyle {\mit\Gamma} = - \frac{2}{[d(\cot\delta_0)/dE]_{E=E_r}}.
$](img2368.png)
![$\displaystyle \frac{d\sigma}{d{\mit\Omega}} = \left(\frac{2\,m_e\,e^2}{4\pi\,\e...
...n_0\,\hbar^{\,2}\,q^2}\right)^2\left(1-\frac{16}{[4+(q\,a_0)^2]^{\,2}}\right),
$](img2370.png)