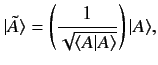Next: Operators
Up: Fundamental Concepts
Previous: Ket Space
A snack machine inputs coins plus some code entered on a key pad, and
(hopefully) outputs a snack. It also does so in a deterministic manner: i.e.,
the same money plus the same code produces the same snack
(or the same error message) time after time.
Note that the input and output of the machine have completely different natures.
We can imagine building a rather abstract snack machine which inputs ket
vectors and outputs complex numbers in a deterministic fashion. Mathematicians
call such a machine a functional. Imagine a general functional, labeled
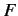 , acting on a general ket vector, labeled
, acting on a general ket vector, labeled  , and spitting out a general
complex number
, and spitting out a general
complex number 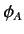 . This process is represented mathematically by writing
. This process is represented mathematically by writing
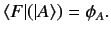 |
(9) |
Let us narrow our focus to those functionals that preserve the linear dependencies
of the ket vectors upon which they operate. Not surprisingly, such functionals
are termed linear functionals. A general linear functional, labeled 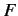 ,
satisfies
,
satisfies
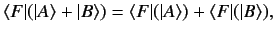 |
(10) |
where  and
and 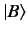 are any two kets in a given ket space.
are any two kets in a given ket space.
Consider an 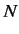 -dimensional ket space [i.e., a finite-dimensional, or
denumerably infinite dimensional (i.e.,
-dimensional ket space [i.e., a finite-dimensional, or
denumerably infinite dimensional (i.e.,
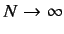 ), space].
Let the
), space].
Let the 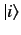 (where
(where 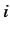 runs from 1 to
runs from 1 to 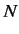 )
represent
)
represent 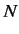 independent ket vectors in this space.
A general ket vector can be written
independent ket vectors in this space.
A general ket vector can be written![[*]](footnote.png)
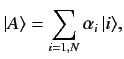 |
(11) |
where the 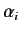 are an arbitrary set of complex numbers.
The only way that the functional
are an arbitrary set of complex numbers.
The only way that the functional 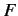 can satisfy Equation (10) for all vectors in the ket
space is if
can satisfy Equation (10) for all vectors in the ket
space is if
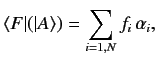 |
(12) |
where the 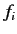 are a set of complex numbers relating to the functional.
are a set of complex numbers relating to the functional.
Let us define 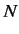 basis functionals
basis functionals
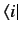 which satisfy
which satisfy
 |
(13) |
Here, the Kronecker delta symbol is defined such that
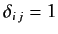 if
if 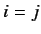 , and
, and
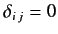 otherwise.
It follows from the previous three equations that
otherwise.
It follows from the previous three equations that
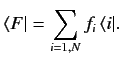 |
(14) |
But, this implies that the set of all possible linear functionals acting
on an 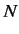 -dimensional ket space is itself an
-dimensional ket space is itself an 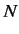 -dimensional vector space.
This type of vector
space is called a bra
space (after Dirac), and its constituent vectors
(which are actually functionals of the ket space) are called bra vectors.
Note that bra vectors are
quite different in nature to ket vectors (hence, these
vectors are written in mirror image notation,
-dimensional vector space.
This type of vector
space is called a bra
space (after Dirac), and its constituent vectors
(which are actually functionals of the ket space) are called bra vectors.
Note that bra vectors are
quite different in nature to ket vectors (hence, these
vectors are written in mirror image notation,
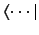 and
and
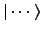 , so that they can never be confused).
Bra space is an example of what mathematicians call a dual
vector space (i.e., it is dual to the original ket space). There is
a one to one correspondence between the elements of the ket space and those
of the related bra space. So, for every element
, so that they can never be confused).
Bra space is an example of what mathematicians call a dual
vector space (i.e., it is dual to the original ket space). There is
a one to one correspondence between the elements of the ket space and those
of the related bra space. So, for every element  of the
ket space, there is a corresponding element, which it is also convenient to
label
of the
ket space, there is a corresponding element, which it is also convenient to
label  , in the bra space. That is,
, in the bra space. That is,
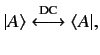 |
(15) |
where DC stands for dual correspondence.
There are an infinite number of ways of setting up the correspondence between
vectors in a ket space and those in the related bra space. However,
only one of these has any physical significance. (See Section 1.11.) For a general ket vector
 , specified by Equation (11), the corresponding bra vector is written
, specified by Equation (11), the corresponding bra vector is written
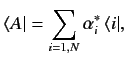 |
(16) |
where the
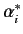 are the complex conjugates of the
are the complex conjugates of the 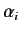 .
.
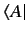 is termed the dual vector to
is termed the dual vector to  . It follows, from the
above, that the dual to
. It follows, from the
above, that the dual to
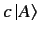 is
is
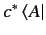 , where
, where  is
a complex number. More generally,
is
a complex number. More generally,
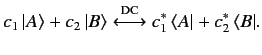 |
(17) |
Recall that a bra vector is a functional that acts on a general ket vector,
and spits out a complex number. Consider the functional which is dual to the
ket vector
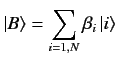 |
(18) |
acting on the ket vector  . This
operation is denoted
. This
operation is denoted
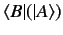 . Note, however, that
we can omit the round brackets without causing any ambiguity, so the
operation can also be written
. Note, however, that
we can omit the round brackets without causing any ambiguity, so the
operation can also be written
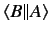 . This
expression can be further simplified
to give
. This
expression can be further simplified
to give
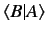 . According to Equations (11), (13), (16),
and (18),
. According to Equations (11), (13), (16),
and (18),
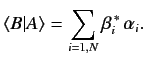 |
(19) |
Mathematicians term
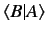 the inner product of a bra and a ket.
the inner product of a bra and a ket.![[*]](footnote.png) An inner product is (almost) analogous to a
scalar product between covariant and contravariant vectors in
curvilinear coordinates.
It is easily demonstrated that
An inner product is (almost) analogous to a
scalar product between covariant and contravariant vectors in
curvilinear coordinates.
It is easily demonstrated that
 |
(20) |
Consider the special case where
 . It
follows from Equations (19) and (20)
that
. It
follows from Equations (19) and (20)
that
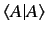 is a real number, and that
is a real number, and that
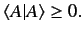 |
(21) |
The equality sign only holds if  is the null ket [i.e., if
all of the
is the null ket [i.e., if
all of the 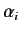 are zero in Equation (11)]. This property of bra and ket
vectors is essential for the probabilistic interpretation of quantum mechanics,
as will become apparent in Section 1.11.
are zero in Equation (11)]. This property of bra and ket
vectors is essential for the probabilistic interpretation of quantum mechanics,
as will become apparent in Section 1.11.
Two kets  and
and
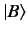 are said to be orthogonal
if
are said to be orthogonal
if
 |
(22) |
which also implies that
 .
.
Given a ket  , which is not the null ket,
we can define a normalized ket
, which is not the null ket,
we can define a normalized ket
 , where
, where
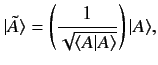 |
(23) |
with the property
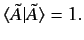 |
(24) |
Here,
 is known as the norm
or ``length'' of
is known as the norm
or ``length'' of  , and
is analogous to the length, or magnitude, of a conventional vector. Because
, and
is analogous to the length, or magnitude, of a conventional vector. Because
 and
and
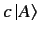 represent the same physical state, it makes sense
to require that all kets corresponding to physical states have unit norms.
represent the same physical state, it makes sense
to require that all kets corresponding to physical states have unit norms.
It is possible to define a dual bra space for a ket space of nondenumerably
infinite dimensions in much the same manner as that described above. The
main differences are that summations over discrete labels become integrations
over continuous labels, Kronecker delta symbols become Dirac delta functions,
completeness must be assumed (it cannot be proved), and the normalization convention
is somewhat different. (See Section 1.15.)



Next: Operators
Up: Fundamental Concepts
Previous: Ket Space
Richard Fitzpatrick
2013-04-08
![]() -dimensional ket space [i.e., a finite-dimensional, or
denumerably infinite dimensional (i.e.,
-dimensional ket space [i.e., a finite-dimensional, or
denumerably infinite dimensional (i.e.,
![]() ), space].
Let the
), space].
Let the ![]() (where
(where ![]() runs from 1 to
runs from 1 to ![]() )
represent
)
represent ![]() independent ket vectors in this space.
A general ket vector can be written
independent ket vectors in this space.
A general ket vector can be written![[*]](footnote.png)
![]() basis functionals
basis functionals
![]() which satisfy
which satisfy
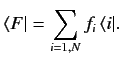

![]() , specified by Equation (11), the corresponding bra vector is written
, specified by Equation (11), the corresponding bra vector is written

![[*]](footnote.png) An inner product is (almost) analogous to a
scalar product between covariant and contravariant vectors in
curvilinear coordinates.
It is easily demonstrated that
An inner product is (almost) analogous to a
scalar product between covariant and contravariant vectors in
curvilinear coordinates.
It is easily demonstrated that
![]() and
and
![]() are said to be orthogonal
if
are said to be orthogonal
if
![]() , which is not the null ket,
we can define a normalized ket
, which is not the null ket,
we can define a normalized ket
![]() , where
, where