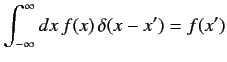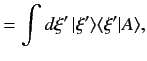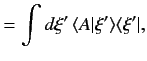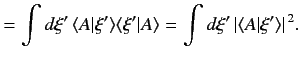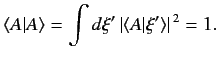Next: Exercises
Up: Fundamental Concepts
Previous: Uncertainty Relation
Continuous Spectra
Up to now, we have studiously avoided dealing with observables possessing
eigenvalues that lie in a continuous range, rather than having discrete
values. The reason for this is that continuous eigenvalues imply a
ket space of nondenumerably infinite dimension. Unfortunately, continuous
eigenvalues are unavoidable in quantum mechanics. In fact, the most important
observables of all--namely position and momentum--generally have continuous
eigenvalues. Fortunately, many of the results that we obtained previously
for a finite-dimensional ket space with discrete eigenvalues can be
generalized to ket spaces of nondenumerably infinite dimensions.
Suppose that  is an observable with continuous eigenvalues. We can still
write the eigenvalue equation as
is an observable with continuous eigenvalues. We can still
write the eigenvalue equation as
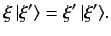 |
(84) |
But, 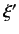 can now take a continuous range of values. Let us assume, for
the sake of simplicity, that
can now take a continuous range of values. Let us assume, for
the sake of simplicity, that 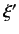 can take any value. The orthogonality
condition (50) generalizes to
can take any value. The orthogonality
condition (50) generalizes to
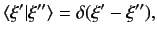 |
(85) |
where 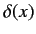 denotes the famous Dirac delta function, and
satisfies
denotes the famous Dirac delta function, and
satisfies
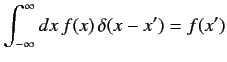 |
(86) |
for any function, 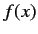 , that is well-behaved at
, that is well-behaved at 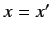 .
Note that there are
clearly a nondenumerably infinite number of mutually orthogonal eigenstates of
.
Note that there are
clearly a nondenumerably infinite number of mutually orthogonal eigenstates of  .
Hence, the dimensionality of ket space is nondenumerably infinite. Furthermore, eigenstates corresponding to a continuous range of eigenvalues cannot
be normalized such that they have unit norms. In fact, these eigenstates have
infinite norms: i.e., they are infinitely long. This is the major difference
between eigenstates in a finite-dimensional and an infinite-dimensional ket space.
The extremely useful relation (54) generalizes to
.
Hence, the dimensionality of ket space is nondenumerably infinite. Furthermore, eigenstates corresponding to a continuous range of eigenvalues cannot
be normalized such that they have unit norms. In fact, these eigenstates have
infinite norms: i.e., they are infinitely long. This is the major difference
between eigenstates in a finite-dimensional and an infinite-dimensional ket space.
The extremely useful relation (54) generalizes to
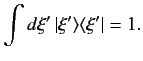 |
(87) |
Note that a summation over discrete eigenvalues goes over into an integral over
a continuous range of eigenvalues. The eigenstates
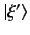 must form
a complete set if
must form
a complete set if  is to be an observable. It follows that any general
ket can be expanded in terms of the
is to be an observable. It follows that any general
ket can be expanded in terms of the
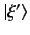 . In fact, the expansions
(51)-(53) generalize to
. In fact, the expansions
(51)-(53) generalize to
These results also follow simply from Equation (87). We have seen that it is not
possible to normalize the eigenstates
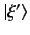 such that they have unit norms.
Fortunately, this convenient normalization is still
possible for a general state vector.
In fact, according to Equation (90), the normalization condition can be written
such that they have unit norms.
Fortunately, this convenient normalization is still
possible for a general state vector.
In fact, according to Equation (90), the normalization condition can be written
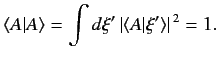 |
(91) |
We have now studied observables whose eigenvalues take a discrete number of
values, as well as those whose eigenvalues take a continuous range of values. There are
a number of other cases
we could look at. For instance, observables whose eigenvalues can take a
(finite) continuous range of values, plus a set of discrete values. Such cases can be
dealt with using a fairly straightforward generalization of the previous
analysis (see Dirac, Chapters II and III).



Next: Exercises
Up: Fundamental Concepts
Previous: Uncertainty Relation
Richard Fitzpatrick
2013-04-08
![]() is an observable with continuous eigenvalues. We can still
write the eigenvalue equation as
is an observable with continuous eigenvalues. We can still
write the eigenvalue equation as