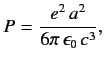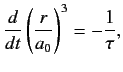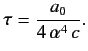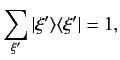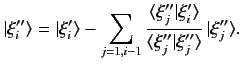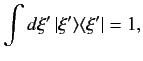Next: Position and Momentum
Up: Fundamental Concepts
Previous: Continuous Spectra
- According to classical physics, a non-relativistic electron whose instantaneous acceleration is of magnitude
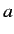 radiates
electromagnetic energy at the rate
radiates
electromagnetic energy at the rate
where 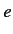 is the magnitude of the electron charge,
is the magnitude of the electron charge,
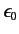 the permittivity of the vacuum, and
the permittivity of the vacuum, and 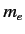 the
electron mass. Consider a classical electron in a
circular orbit of radius
the
electron mass. Consider a classical electron in a
circular orbit of radius 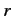 around a proton. Demonstrate that the radiated energy would cause the orbital radius to decrease in time according to
around a proton. Demonstrate that the radiated energy would cause the orbital radius to decrease in time according to
where
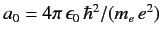 is the Bohr radius,
is the Bohr radius, 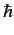 the reduced Planck constant, and
the reduced Planck constant, and
Here, 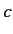 is the velocity of light in a vacuum, and
is the velocity of light in a vacuum, and
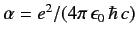 the fine structure constant.
Deduce that the classical lifetime of a hydrogen atom is
the fine structure constant.
Deduce that the classical lifetime of a hydrogen atom is
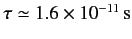 .
.
- Demonstrate that
in a finite dimensional ket space.
- Demonstrate that in a finite dimensional ket space:
Here, 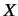 ,
, 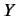 are general operators.
are general operators.
- If
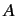 ,
, 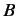 are Hermitian operators then demonstrate that
are Hermitian operators then demonstrate that 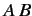 is only Hermitian provided
is only Hermitian provided 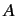 and
and 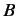 commute. In addition, show that
commute. In addition, show that 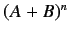 is Hermitian, where
is Hermitian, where 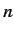 is a positive integer.
is a positive integer.
- Let
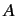 be a general operator. Show that
be a general operator. Show that 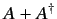 ,
,
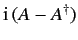 , and
, and 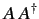 are Hermitian operators.
are Hermitian operators.
- Let
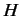 be an Hermitian operator. Demonstrate that the Hermitian conjugate of the operator
be an Hermitian operator. Demonstrate that the Hermitian conjugate of the operator
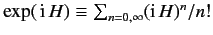 is
is
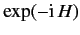 .
.
- Let the
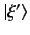 be the eigenkets of an observable
be the eigenkets of an observable  , whose corresponding eigenvalues,
, whose corresponding eigenvalues, 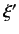 , are discrete.
Demonstrate that
, are discrete.
Demonstrate that
where the sum is over all eigenvalues, and 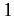 denotes the unity operator.
denotes the unity operator.
- Let the
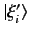 , where
, where 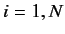 , and
, and 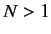 , be a set of degenerate eigenkets of some
observable
, be a set of degenerate eigenkets of some
observable  . Suppose that the
. Suppose that the
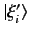 are not mutually orthogonal. Demonstrate that a set of
mutually orthogonal (but unnormalized) degenerate eigenkets,
are not mutually orthogonal. Demonstrate that a set of
mutually orthogonal (but unnormalized) degenerate eigenkets,
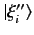 , for
, for 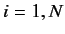 , can be constructed as follows:
, can be constructed as follows:
This process is known as Gram-Schmidt orthogonalization.
- Demonstrate that the expectation value of a Hermitian operator is a real number. Show that the
expectation value of an anti-hermitian operator is an imaginary number.
- Let
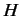 be an Hermitian operator. Demonstrate that
be an Hermitian operator. Demonstrate that
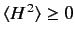 .
.
- Consider an Hermitian operator,
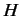 , that has the property that
, that has the property that 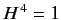 , where
, where 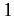 is the unity
operator. What are the eigenvalues of
is the unity
operator. What are the eigenvalues of 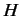 ? What are the eigenvalues if
? What are the eigenvalues if 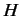 is not restricted to
being Hermitian?
is not restricted to
being Hermitian?
- Let
 be an observable whose eigenvalues,
be an observable whose eigenvalues, 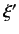 , lie in a continuous range. Let the
, lie in a continuous range. Let the
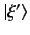 , where
, where
be the corresponding eigenkets. Demonstrate that
where the integral is over the whole range of eigenvalues, and 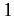 denotes the unity operator.
denotes the unity operator.



Next: Position and Momentum
Up: Fundamental Concepts
Previous: Continuous Spectra
Richard Fitzpatrick
2013-04-08