


Next: Outer Product
Up: Fundamental Concepts
Previous: Bra Space
We have seen that a functional is a machine that inputs a ket vector and
spits out a complex number. Consider a
somewhat different machine that inputs a ket
vector and spits out another ket vector in a deterministic fashion. Mathematicians
call such a machine an operator. We are only interested in operators
that preserve the linear dependencies of the ket vectors upon which
they act. Such operators are termed linear operators. Consider an operator
labeled 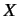 . Suppose that when this operator acts on a general ket vector
. Suppose that when this operator acts on a general ket vector
 it spits out a new ket vector which is denoted
it spits out a new ket vector which is denoted
 . Operator
. Operator 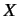 is linear provided that
is linear provided that
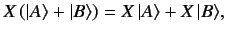 |
(25) |
for all ket vectors  and
and
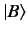 , and
, and
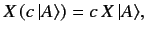 |
(26) |
for all complex numbers  . Operators
. Operators 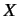 and
and 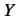 are said to be equal
if
are said to be equal
if
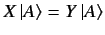 |
(27) |
for all kets in the ket space in question. Operator 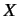 is termed the
null operator
if
is termed the
null operator
if
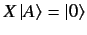 |
(28) |
for all ket vectors in the space. Operators can be added together. Such addition
is defined to obey a commutative and associate algebra: i.e.,
Operators can also be multiplied. The multiplication is associative:
However, in general, it is non-commutative: i.e.,
 |
(33) |
So far, we have only considered linear operators acting on ket vectors. We can also
give a meaning to their operation on bra vectors. Consider the inner product
of a general bra
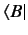 with the ket
with the ket
 . This product is a
number that depends linearly on
. This product is a
number that depends linearly on  . Thus, it may be considered to
be the inner product of
. Thus, it may be considered to
be the inner product of  with some bra. This bra depends linearly
on
with some bra. This bra depends linearly
on
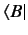 , so we may look on it as the result of some linear
operator applied to
, so we may look on it as the result of some linear
operator applied to
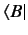 . This operator is uniquely determined by the
original operator
. This operator is uniquely determined by the
original operator 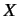 , so we might as well call it the same operator acting on
, so we might as well call it the same operator acting on
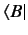 . A suitable notation to use for the resulting bra when
. A suitable notation to use for the resulting bra when 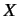 operates on
operates on
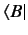 is
is
 . The equation which defines this
vector is
. The equation which defines this
vector is
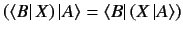 |
(34) |
for any  and
and
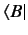 .
The triple product of
.
The triple product of
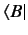 ,
, 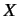 , and
, and  can be written
can be written
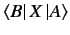 without ambiguity, provided we adopt the
convention that the bra vector always goes on the left, the operator in the middle,
and the ket vector on the right.
without ambiguity, provided we adopt the
convention that the bra vector always goes on the left, the operator in the middle,
and the ket vector on the right.
Consider the dual bra to
 . This bra depends antilinearly on
. This bra depends antilinearly on
 and must therefore depend linearly on
and must therefore depend linearly on
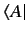 .
Thus, it may
be regarded as the result of some linear operator applied to
.
Thus, it may
be regarded as the result of some linear operator applied to
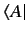 .
This operator is termed the adjoint of
.
This operator is termed the adjoint of 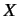 , and is denoted
, and is denoted 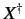 . Thus,
. Thus,
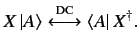 |
(35) |
It is readily demonstrated that
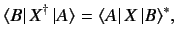 |
(36) |
plus
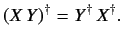 |
(37) |
It is also easily seen that the adjoint of the adjoint of a linear operator
is equivalent to the original operator. An Hermitian operator  has
the special property that it is its own adjoint: i.e.,
has
the special property that it is its own adjoint: i.e.,
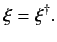 |
(38) |



Next: Outer Product
Up: Fundamental Concepts
Previous: Bra Space
Richard Fitzpatrick
2013-04-08
![]() with the ket
with the ket
![]() . This product is a
number that depends linearly on
. This product is a
number that depends linearly on ![]() . Thus, it may be considered to
be the inner product of
. Thus, it may be considered to
be the inner product of ![]() with some bra. This bra depends linearly
on
with some bra. This bra depends linearly
on
![]() , so we may look on it as the result of some linear
operator applied to
, so we may look on it as the result of some linear
operator applied to
![]() . This operator is uniquely determined by the
original operator
. This operator is uniquely determined by the
original operator ![]() , so we might as well call it the same operator acting on
, so we might as well call it the same operator acting on
![]() . A suitable notation to use for the resulting bra when
. A suitable notation to use for the resulting bra when ![]() operates on
operates on
![]() is
is
![]() . The equation which defines this
vector is
. The equation which defines this
vector is
![]() . This bra depends antilinearly on
. This bra depends antilinearly on
![]() and must therefore depend linearly on
and must therefore depend linearly on
![]() .
Thus, it may
be regarded as the result of some linear operator applied to
.
Thus, it may
be regarded as the result of some linear operator applied to
![]() .
This operator is termed the adjoint of
.
This operator is termed the adjoint of ![]() , and is denoted
, and is denoted ![]() . Thus,
. Thus,