


Next: Spontaneous Emission
Up: Time-Dependent Perturbation Theory
Previous: Absorption and Stimulated Emission
Electric Dipole Approximation
In general, the wavelength of the type of
electromagnetic radiation that induces, or is emitted during, transitions
between different atomic energy levels is much larger than the
typical size of
a light atom. Thus,
![$\displaystyle \exp[\,{\rm i}\,(\omega/c)\,{\bf n}\cdot{\bf x}] = 1 + {\rm i}\,\frac{\omega}{c} \,{\bf n}\cdot{\bf x} + \cdots,$](img2070.png) |
(887) |
can be approximated by its first term, unity (remember that
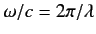 ).
This approximation is known as the electric dipole approximation.
It follows that
).
This approximation is known as the electric dipole approximation.
It follows that
It is readily demonstrated that
![$\displaystyle [{\bf x}, H_0] = \frac{{\rm i}\, \hbar \,{\bf p}}{m_e},$](img2075.png) |
(889) |
so
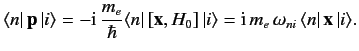 |
(890) |
Thus, making use of the electric dipole approximation, we obtain
for absorption, and
for stimulated emission, where
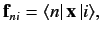 |
(893) |
and
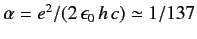 is the fine structure constant.
is the fine structure constant.
Suppose that the radiation is polarized in the 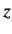 -direction,
so that
-direction,
so that
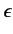
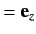 . We have already seen, from Section 7.4, that
. We have already seen, from Section 7.4, that
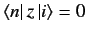 unless the initial and final states satisfy
unless the initial and final states satisfy
Here, 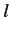 is the quantum number describing the total orbital angular momentum of
the electron, and
is the quantum number describing the total orbital angular momentum of
the electron, and 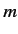 is the quantum number describing the projection of the
orbital angular momentum along the
is the quantum number describing the projection of the
orbital angular momentum along the 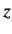 -axis.
It is easily demonstrated that
-axis.
It is easily demonstrated that
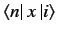 and
and
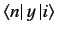 are only non-zero if
are only non-zero if
Thus, for generally directed radiation
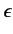
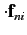 is only non-zero if
is only non-zero if
These are termed the selection rules for electric dipole transitions. It
is clear, for instance, that the electric dipole approximation allows
a transition from a 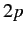 state to a
state to a 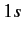 state, but disallows a transition
from a
state, but disallows a transition
from a 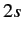 to a
to a 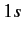 state. The latter transition is called a forbidden
transition.
state. The latter transition is called a forbidden
transition.
Forbidden transitions are not strictly forbidden. Instead, they take
place at a far lower rate than transitions that are allowed
according to the electric
dipole approximation.
After electric dipole transitions, the next most likely type of transition
is a magnetic dipole transition, which is due to the interaction between
the electron spin and the oscillating magnetic field of the
incident electromagnetic
radiation. Magnetic dipole transitions are typically about 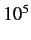 times
more unlikely than similar electric dipole transitions. The first-order term
in Equation (887) yields so-called electric quadrupole transitions.
These are typically about
times
more unlikely than similar electric dipole transitions. The first-order term
in Equation (887) yields so-called electric quadrupole transitions.
These are typically about 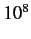 times more unlikely than electric
dipole transitions. Magnetic dipole and electric quadrupole transitions
satisfy different selection rules than electric dipole transitions. For instance, the selection rules for electric quadrupole transitions
are
times more unlikely than electric
dipole transitions. Magnetic dipole and electric quadrupole transitions
satisfy different selection rules than electric dipole transitions. For instance, the selection rules for electric quadrupole transitions
are
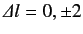 . Thus, transitions that are forbidden as
electric dipole transitions may well be allowed as magnetic dipole
or electric quadrupole transitions.
. Thus, transitions that are forbidden as
electric dipole transitions may well be allowed as magnetic dipole
or electric quadrupole transitions.



Next: Spontaneous Emission
Up: Time-Dependent Perturbation Theory
Previous: Absorption and Stimulated Emission
Richard Fitzpatrick
2013-04-08
![$\displaystyle \exp[\,{\rm i}\,(\omega/c)\,{\bf n}\cdot{\bf x}] = 1 + {\rm i}\,\frac{\omega}{c} \,{\bf n}\cdot{\bf x} + \cdots,$](img2070.png)
![$\displaystyle [{\bf x}, H_0] = \frac{{\rm i}\, \hbar \,{\bf p}}{m_e},$](img2075.png)
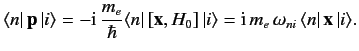
![]() -direction,
so that
-direction,
so that
![]()
![]() . We have already seen, from Section 7.4, that
. We have already seen, from Section 7.4, that
![]() unless the initial and final states satisfy
unless the initial and final states satisfy
![]() times
more unlikely than similar electric dipole transitions. The first-order term
in Equation (887) yields so-called electric quadrupole transitions.
These are typically about
times
more unlikely than similar electric dipole transitions. The first-order term
in Equation (887) yields so-called electric quadrupole transitions.
These are typically about ![]() times more unlikely than electric
dipole transitions. Magnetic dipole and electric quadrupole transitions
satisfy different selection rules than electric dipole transitions. For instance, the selection rules for electric quadrupole transitions
are
times more unlikely than electric
dipole transitions. Magnetic dipole and electric quadrupole transitions
satisfy different selection rules than electric dipole transitions. For instance, the selection rules for electric quadrupole transitions
are
![]() . Thus, transitions that are forbidden as
electric dipole transitions may well be allowed as magnetic dipole
or electric quadrupole transitions.
. Thus, transitions that are forbidden as
electric dipole transitions may well be allowed as magnetic dipole
or electric quadrupole transitions.