


Next: Exercises
Up: Time-Dependent Perturbation Theory
Previous: Electric Dipole Approximation
So far, we have calculated the rates of radiation induced transitions
between two atomic states. This process is known as absorption when the energy of the final state exceeds that
of the initial state, and stimulated emission when the energy of the final state is less than that
of the initial state. Now, in the absence of any external radiation, we would
not expect an atom in a given state to spontaneously jump into a
state with a higher energy. On the other hand, it should be possible for
such an atom to spontaneously jump into an state with a lower energy
via the emission of a photon whose energy is equal to the difference
between the energies of the initial and final states. This process is known as spontaneous emission.
It is possible to derive the rate of spontaneous emission between two atomic states
from a knowledge of the corresponding absorption and stimulated
emission rates using a famous thermodynamic argument due to Einstein.
Consider a very large ensemble of similar atoms placed inside a closed cavity whose walls (which are assumed to be perfect emitters and absorbers of radiation) are held at
the constant temperature 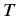 . Let the system have attained thermal equilibrium.
According to statistical thermodynamics, the cavity is filled with so-called ``black-body'' electromagnetic
radiation whose energy spectrum is
. Let the system have attained thermal equilibrium.
According to statistical thermodynamics, the cavity is filled with so-called ``black-body'' electromagnetic
radiation whose energy spectrum is
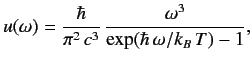 |
(900) |
where 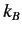 is the Boltzmann constant. This well-known result was first
obtained by Max Planck in 1900.
is the Boltzmann constant. This well-known result was first
obtained by Max Planck in 1900.
Consider two atomic states, labeled  and
and 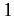 , with
, with 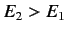 . One
of the tenants of statistical thermodynamics is that in thermal equilibrium
we have so-called detailed balance. This means that, irrespective
of any other atomic states, the rate at which atoms in the ensemble leave
state
. One
of the tenants of statistical thermodynamics is that in thermal equilibrium
we have so-called detailed balance. This means that, irrespective
of any other atomic states, the rate at which atoms in the ensemble leave
state 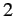 due to transitions to state
due to transitions to state 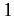 is exactly balanced by the
rate at which atoms enter state
is exactly balanced by the
rate at which atoms enter state 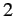 due to transitions from state
due to transitions from state 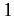 .
The former rate (i.e., number of transitions per unit time in the ensemble) is written
.
The former rate (i.e., number of transitions per unit time in the ensemble) is written
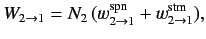 |
(901) |
where
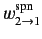 and
and
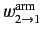 are the rates of spontaneous and stimulated emission,
respectively,
(for a single atom) between
states
are the rates of spontaneous and stimulated emission,
respectively,
(for a single atom) between
states 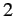 and
and 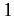 , and
, and 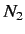 is the number of atoms in the ensemble
in state
is the number of atoms in the ensemble
in state 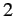 . Likewise, the latter rate takes the form
. Likewise, the latter rate takes the form
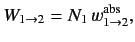 |
(902) |
where
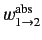 is the rate of absorption (for a single atom) between states
is the rate of absorption (for a single atom) between states 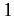 and
and 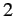 , and
, and 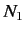 is the number of atoms in the ensemble in state
is the number of atoms in the ensemble in state 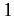 .
The above expressions describe how atoms in the ensemble make transitions from
state
.
The above expressions describe how atoms in the ensemble make transitions from
state 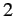 to state
to state 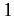 due to a combination of spontaneous and stimulated emission, and make the opposite transition as a consequence of absorption.
In thermal equilibrium, we have
due to a combination of spontaneous and stimulated emission, and make the opposite transition as a consequence of absorption.
In thermal equilibrium, we have
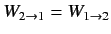 ,
which gives
,
which gives
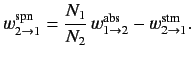 |
(903) |
Equations (891) and (892) imply that
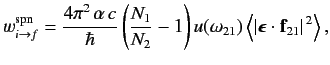 |
(904) |
where
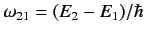 , and the large angle brackets denote an average over all possible directions of the incident radiation (because, in equilibrium, the
radiation inside the cavity is isotropic).
In fact, it is easily demonstrated that
, and the large angle brackets denote an average over all possible directions of the incident radiation (because, in equilibrium, the
radiation inside the cavity is isotropic).
In fact, it is easily demonstrated that
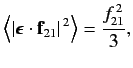 |
(905) |
where
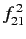 stands for
stands for
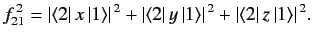 |
(906) |
Now, another famous result in statistical thermodynamics is that
in thermal equilibrium the number of atoms in an ensemble occupying
a state of energy 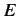 is proportional to
is proportional to
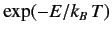 . This implies
that
. This implies
that
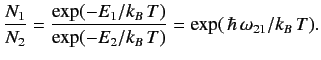 |
(907) |
Thus, it follows from Equations (900), (904), (905), and (907) that the rate of spontaneous emission between states
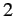 and
and 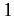 takes the form
takes the form
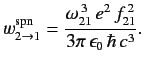 |
(908) |
Note, that, although the above result has been derived for
an atom in a radiation-filled cavity, it remains correct even in the absence
of radiation.
Let us estimate the typical value of the spontaneous emission rate for a
hydrogen atom. We expect the matrix element 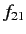 to be
of order
to be
of order 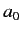 , where
, where 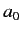 is the Bohr radius.
We also expect
is the Bohr radius.
We also expect
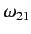 to be of order
to be of order
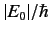 , where
, where 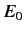 is the ground-state energy. It thus
follows from Equation (908) that
is the ground-state energy. It thus
follows from Equation (908) that
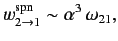 |
(909) |
where
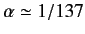 is
the fine structure constant. This is an important result, because our perturbation
expansion is based on the assumption that the transition rate between different energy
eigenstates is much slower than the frequency of phase oscillation of these states:
i.e., that
is
the fine structure constant. This is an important result, because our perturbation
expansion is based on the assumption that the transition rate between different energy
eigenstates is much slower than the frequency of phase oscillation of these states:
i.e., that
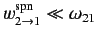 . This is indeed the
case.
. This is indeed the
case.



Next: Exercises
Up: Time-Dependent Perturbation Theory
Previous: Electric Dipole Approximation
Richard Fitzpatrick
2013-04-08
![]() . Let the system have attained thermal equilibrium.
According to statistical thermodynamics, the cavity is filled with so-called ``black-body'' electromagnetic
radiation whose energy spectrum is
. Let the system have attained thermal equilibrium.
According to statistical thermodynamics, the cavity is filled with so-called ``black-body'' electromagnetic
radiation whose energy spectrum is
![]() and
and ![]() , with
, with ![]() . One
of the tenants of statistical thermodynamics is that in thermal equilibrium
we have so-called detailed balance. This means that, irrespective
of any other atomic states, the rate at which atoms in the ensemble leave
state
. One
of the tenants of statistical thermodynamics is that in thermal equilibrium
we have so-called detailed balance. This means that, irrespective
of any other atomic states, the rate at which atoms in the ensemble leave
state ![]() due to transitions to state
due to transitions to state ![]() is exactly balanced by the
rate at which atoms enter state
is exactly balanced by the
rate at which atoms enter state ![]() due to transitions from state
due to transitions from state ![]() .
The former rate (i.e., number of transitions per unit time in the ensemble) is written
.
The former rate (i.e., number of transitions per unit time in the ensemble) is written
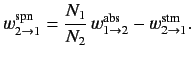
![]() to be
of order
to be
of order ![]() , where
, where ![]() is the Bohr radius.
We also expect
is the Bohr radius.
We also expect
![]() to be of order
to be of order
![]() , where
, where ![]() is the ground-state energy. It thus
follows from Equation (908) that
is the ground-state energy. It thus
follows from Equation (908) that