


Next: Fine Structure
Up: Time-Independent Perturbation Theory
Previous: Degenerate Perturbation Theory
Linear Stark Effect
Let us examine the effect of an electric field on the excited energy
levels of a hydrogen atom. For instance, consider the 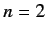 states.
There is a single
states.
There is a single 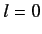 state, usually referred to as
state, usually referred to as 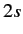 , and three
, and three 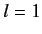 states (with
states (with 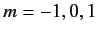 ), usually referred to as
), usually referred to as 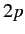 . All of these states
possess the same energy,
. All of these states
possess the same energy,
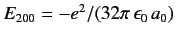 . As in Section 7.4, the
perturbing Hamiltonian is
. As in Section 7.4, the
perturbing Hamiltonian is
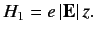 |
(663) |
In order to apply perturbation theory, we have to solve
the matrix eigenvalue equation
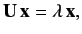 |
(664) |
where 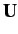 is the array of the matrix elements of
is the array of the matrix elements of 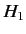 between the
degenerate
between the
degenerate 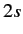 and
and
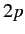 states. Thus,
states. Thus,
 |
(665) |
where the rows and columns correspond to the
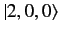 ,
,
 ,
,
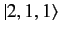 , and
, and
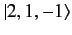 states, respectively. Here, we have made use
of the selection rules, which tell us that the matrix element of
states, respectively. Here, we have made use
of the selection rules, which tell us that the matrix element of  between
two hydrogen atom states is zero unless the states
possess the same
between
two hydrogen atom states is zero unless the states
possess the same  quantum number,
and
quantum number,
and  quantum numbers that differ by unity. It is easily demonstrated,
from the exact forms of the
quantum numbers that differ by unity. It is easily demonstrated,
from the exact forms of the 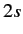 and
and 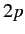 wavefunctions, that
wavefunctions, that
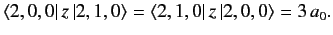 |
(666) |
It can be seen, by inspection, that the eigenvalues of 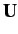 are
are
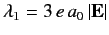 ,
,
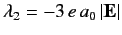 ,
,
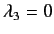 ,
and
,
and
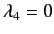 . The corresponding eigenvectors are
. The corresponding eigenvectors are
It follows from Section 7.5 that the
simultaneous eigenstates of the unperturbed Hamiltonian and the
perturbing Hamiltonian take the form
In the absence of an electric field, all of these states possess the
same energy, 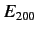 .
The first-order energy-shifts induced by an electric field are
given by
.
The first-order energy-shifts induced by an electric field are
given by
Thus, the energies of states 1 and 2 are shifted upwards and downwards, respectively,
by an amount
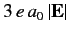 in the presence of an electric field.
States 1 and 2 are orthogonal linear combinations of the original
in the presence of an electric field.
States 1 and 2 are orthogonal linear combinations of the original
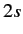 and
and  states.
Note that
the energy-shifts are linear in the electric field-strength, so this
is a much larger effect that the quadratic effect described in Section 7.4.
The energies of states 3 and 4 (which are equivalent to the
original
states.
Note that
the energy-shifts are linear in the electric field-strength, so this
is a much larger effect that the quadratic effect described in Section 7.4.
The energies of states 3 and 4 (which are equivalent to the
original 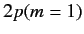 and
and 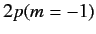 states, respectively)
are not affected to first order. Of course, to second order the energies of these states are shifted by an amount that depends on the
square of the electric field-strength.
states, respectively)
are not affected to first order. Of course, to second order the energies of these states are shifted by an amount that depends on the
square of the electric field-strength.
Note that the linear Stark effect depends crucially on the degeneracy of
the 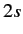 and
and
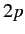 states. This degeneracy is a special property of
a pure Coulomb potential, and, therefore, only applies to a hydrogen atom.
Thus, alkali metal atoms do not exhibit the linear Stark effect.
states. This degeneracy is a special property of
a pure Coulomb potential, and, therefore, only applies to a hydrogen atom.
Thus, alkali metal atoms do not exhibit the linear Stark effect.



Next: Fine Structure
Up: Time-Independent Perturbation Theory
Previous: Degenerate Perturbation Theory
Richard Fitzpatrick
2013-04-08

![]() are
are
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() . The corresponding eigenvectors are
. The corresponding eigenvectors are
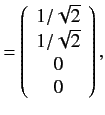
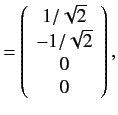
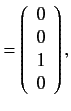
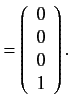
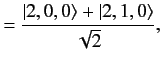
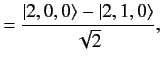
![]() and
and
![]() states. This degeneracy is a special property of
a pure Coulomb potential, and, therefore, only applies to a hydrogen atom.
Thus, alkali metal atoms do not exhibit the linear Stark effect.
states. This degeneracy is a special property of
a pure Coulomb potential, and, therefore, only applies to a hydrogen atom.
Thus, alkali metal atoms do not exhibit the linear Stark effect.