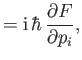 |
||
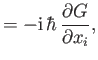 |
where
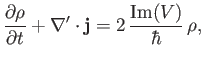
where
and
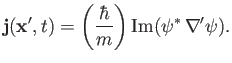
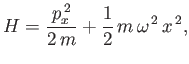
where
- Demonstrate that the expectation value of
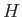 , for a general state, is
positive definite.
, for a general state, is
positive definite.
- Let
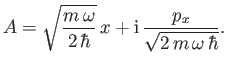
Deduce that![$\displaystyle [A,A^\dag ]$](img832.png)
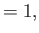
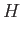
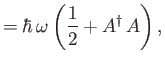
![$\displaystyle [H,A]$](img835.png)
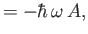
![$\displaystyle [H,A^\dag ]$](img837.png)
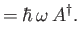
- Suppose that
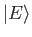 is an eigenket of the Hamiltonian whose corresponding energy is
is an eigenket of the Hamiltonian whose corresponding energy is 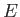 : that is,
: that is,
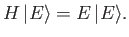
Demonstrate that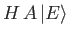
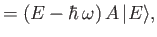
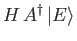
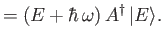
Hence, deduce that the allowed values of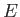 are
are
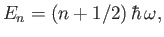
where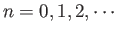 . Here,
. Here, 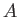 and
and 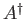 are termed ladder operators. To be more exact,
are termed ladder operators. To be more exact, 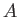 is termed a lowering operator (because it lowers the energy quantum number,
is termed a lowering operator (because it lowers the energy quantum number, 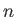 , by unity), whereas
, by unity), whereas
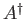 is termed a raising operator (because it raises the energy quantum number by unity).
is termed a raising operator (because it raises the energy quantum number by unity).
- Let
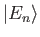 be a properly normalized (i.e.,
be a properly normalized (i.e.,
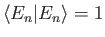 ) energy eigenket corresponding to the
eigenvalue
) energy eigenket corresponding to the
eigenvalue 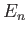 . Show that the kets can be defined such that
. Show that the kets can be defined such that
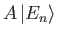
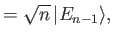
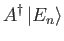
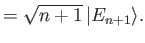
Hence, deduce that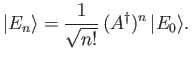
- Let the
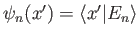 be the wavefunctions of the properly normalized energy eigenkets.
Given that
be the wavefunctions of the properly normalized energy eigenkets.
Given that
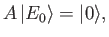
deduce that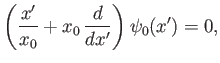
where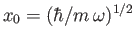 . Hence, show that
. Hence, show that
![$\displaystyle \psi_n(x') = \frac{1}{\pi^{1/4}\,(2^n\,n!)^{1/2}\,x_0^{\,n+1/2}}\...
...c{d}{dx'}\right)^n\exp\left[-\frac{1}{2}\left(
\frac{x'}{x_0}\right)^2\right].
$](img861.png)
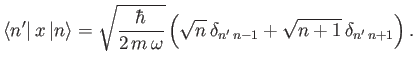
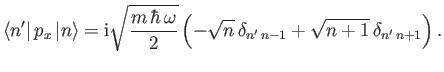
-
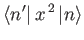
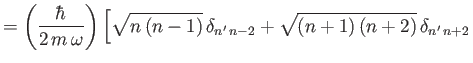
![$\displaystyle \phantom{=}\left.+ (2\,n+1)\,\delta_{n'\,n}\right].$](img867.png)
-
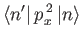
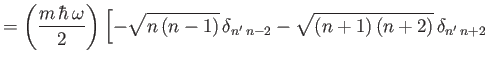
![$\displaystyle \phantom{=}\left.+ (2\,n+1)\,\delta_{n'\,n}\right].$](img867.png)
- Hence, deduce that
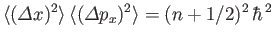
for the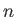 th eigenstate.
th eigenstate.
- Demonstrate that
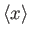
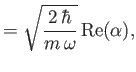
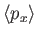
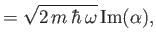
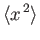
![$\displaystyle = \frac{2\,\hbar}{m\,\omega}\left(\frac{1}{4}+\left[{\rm Re}(\alpha)\right]^2\right),$](img877.png)
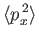
![$\displaystyle = 2\,m\,\hbar\,\omega\left(\frac{1}{4}+\left[{\rm Im}(\alpha)\right]^2\right),$](img879.png)
where the expectation values are relative to the coherent state. Hence, deduce that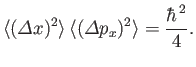
In other words, a coherent state is characterized by the minimum possible uncertainty in position and momentum. - If
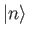 is the properly normalized energy eigenket belonging to the energy eigenvalue
is the properly normalized energy eigenket belonging to the energy eigenvalue
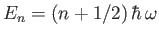 then show that
then show that
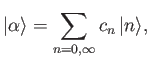
where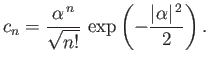
- Show that the expectation value of the energy for the coherent state is
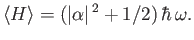
- Putting in time dependence, so that
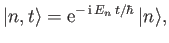
where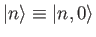 ,
demonstrate that
,
demonstrate that
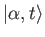 remains an eigenket of
remains an eigenket of 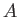 , but that the eigenvalue
evolves in time as
, but that the eigenvalue
evolves in time as
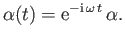
Hence, deduce that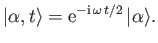
- Writing
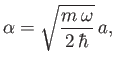
where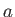 is real and positive, show that
is real and positive, show that
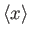
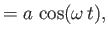
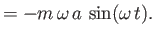
Of course, these expressions are analogous to those of a classical harmonic oscillator of amplitude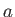 and angular frequency
and angular frequency 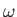 . This suggests that a coherent state
of a quantum harmonic oscillator is the state that most closely imitates the behavior of
a classical oscillator.
. This suggests that a coherent state
of a quantum harmonic oscillator is the state that most closely imitates the behavior of
a classical oscillator.
- Show that the properly normalized wavefunction corresponding to the state
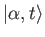 takes the form
takes the form
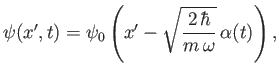
(3.111)
where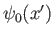 is the properly normalized, stationary, ground-state wavefunction.
is the properly normalized, stationary, ground-state wavefunction.
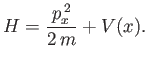
By calculating
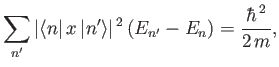
where
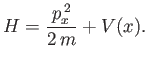
Suppose that the potential is periodic, such that
for all
where
where
respectively. Hence, deduce that the momentum and position operators evolve in time as
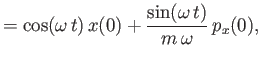 |
respectively, in the Heisenberg picture.
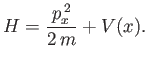
Suppose that the particle is in a stationary bound state. Using the time-independent Schrödinger equation, prove that
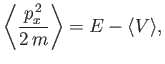
and
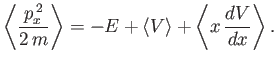
Here,
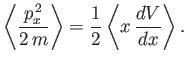
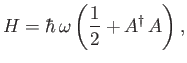
where
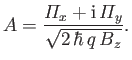
In addition, show that
Hence, deduce that the possible energy eigenstates of the particle are
where
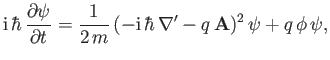
where
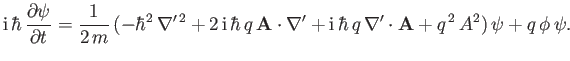
Hence, deduce that if the so-called Coloumb gauge [49],
is adopted then the equation simplifies to
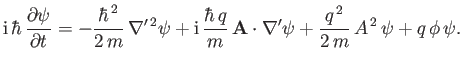
Demonstrate that this equation is associated with a probability conservation law of the form
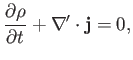
where
and
![$\displaystyle {\bf j}({\bf x}', t) = -\left(\frac{{\rm i}\,\hbar}{2\,m}\right)[...
...\nabla'\psi)^\ast\,\psi]- \frac{q}{m}\,\rho({\bf x}', t)\,{\bf A}({\bf x}',t).
$](img922.png)
Finally, show that