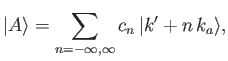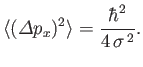Suppose that we displace a one-dimensional quantum mechanical system a finite distance 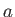 along the
along the  -axis. The
corresponding operator is
-axis. The
corresponding operator is
where 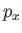 is the momentum conjugate to the position operator
is the momentum conjugate to the position operator  . Demonstrate that
. Demonstrate that
[Hint: Use the momentum
representation,
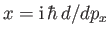 .] Similarly, demonstrate that
.] Similarly, demonstrate that
where 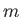 is a non-negative integer.
Hence, deduce that
is a non-negative integer.
Hence, deduce that
where 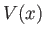 is a function of
is a function of  that can be expanded as a power series.
that can be expanded as a power series.
Let
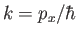 , and let
, and let
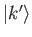 denote an eigenket of the
denote an eigenket of the 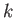 operator belonging to the eigenvalue
operator belonging to the eigenvalue 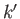 .
Demonstrate that
.
Demonstrate that
where the 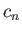 are arbitrary complex coefficients, and
are arbitrary complex coefficients, and
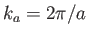 , is an eigenket of the
, is an eigenket of the 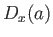 operator
belonging to the eigenvalue
operator
belonging to the eigenvalue
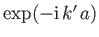 . Show that the corresponding wavefunction can
be written
. Show that the corresponding wavefunction can
be written
where
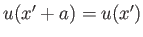 for all
for all 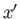 .
.
![$\displaystyle \psi(x') =\psi_0\,\exp\left[-\frac{(x'-x_0)^{\,2}}{4\,\sigma^{\,2}}\right],
$](img560.png)
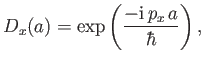
![]() , and let
, and let
![]() denote an eigenket of the
denote an eigenket of the ![]() operator belonging to the eigenvalue
operator belonging to the eigenvalue ![]() .
Demonstrate that
.
Demonstrate that