Our zeroth-order solution is characterized by three undetermined flux-surface functions:
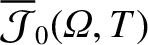 ,
,
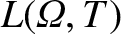 , and
, and
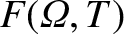 .
In order to determine the forms of these functions, we need to expand our model to higher order. (See Section 8.8.)
.
In order to determine the forms of these functions, we need to expand our model to higher order. (See Section 8.8.)
Expanding Equation (11.68) to third order in 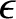 , we obtain
we obtain
, we obtain
we obtain
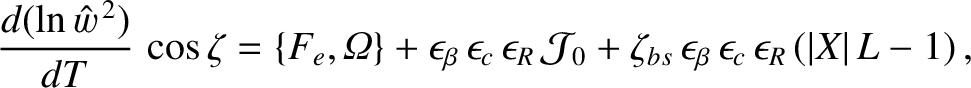 |
(11.124) |
where
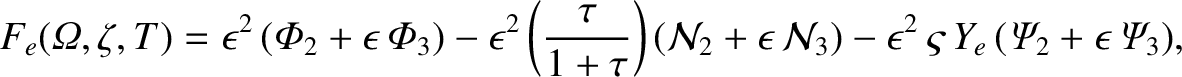 |
(11.125) |
and use has been made of Equations (8.75), (11.95)–(11.99), (11.103), (11.104), (11.107), and (11.108).
The flux-surface average of Equation (11.124) yields
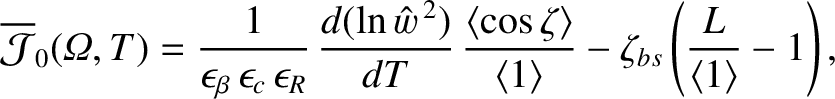 |
(11.126) |
where use has been made of Equations (8.68), (8.70), and (11.114), and (11.116). Note that
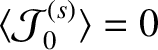 , by symmetry.
Hence,
where use has been made of Equation (11.116).
, by symmetry.
Hence,
where use has been made of Equation (11.116).
Expanding Equation (11.69) to first order in 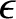 ,
we obtain
,
we obtain
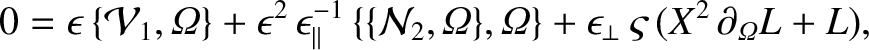 |
(11.128) |
where use has been made of Equations (11.95)–(11.99), (11.101), (11.103), and (11.104). The flux-surface average of the
previous equation yields
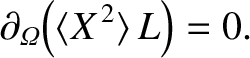 |
(11.129) |
We can solve the previous equation, subject to the boundary condition (11.105), to give
![\begin{displaymath}L({\mit\Omega},T)= L({\mit\Omega})=\left\{
\begin{array}{llr}...
...5ex]
1/\langle X^2\rangle&~~&{\mit\Omega}>1
\end{array}\right..\end{displaymath}](img3578.png) |
(11.130) |
Here, we have taken into account the previously mentioned fact that 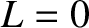 within the island separatrix.
Note that
within the island separatrix.
Note that
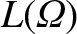 is discontinuous across the island separatrix, which implies that the pressure gradient is also discontinuous across the separatrix. As discussed in Section 8.9, we expect this discontinuity to be resolved in a layer of characteristic thickness
is discontinuous across the island separatrix, which implies that the pressure gradient is also discontinuous across the separatrix. As discussed in Section 8.9, we expect this discontinuity to be resolved in a layer of characteristic thickness 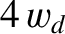 on the separatrix [see Equation (8.84) and Table 8.1].
on the separatrix [see Equation (8.84) and Table 8.1].
Expanding Equation (11.71) to second order in 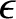 , we obtain
we obtain
, we obtain
we obtain
| 0 |
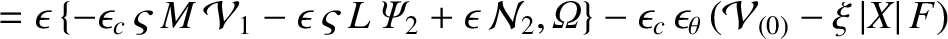 |
|
| |
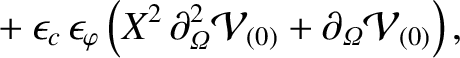 |
(11.131) |
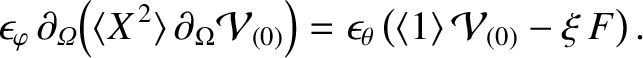 |
(11.132) |
According to Equation (11.121), recalling that
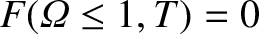 , we get
, we get
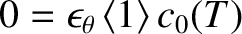 |
(11.133) |
inside the separatrix, which implies that 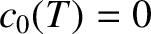 . Hence, given that we have already concluded that
. Hence, given that we have already concluded that 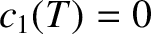 , Equations (11.121) and
(11.122) yield
, Equations (11.121) and
(11.122) yield
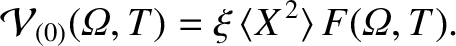 |
(11.134) |
The previous equation can be combined with Equation (11.132) to produce
![$\displaystyle \epsilon_\varphi\,\partial_{\mit\Omega}\!\left[\langle X^{\,2}\ra...
...ht] = \epsilon_\theta\left(\langle X^{\,2}\rangle\,\langle 1\rangle -1\right)F.$](img3585.png) |
(11.135) |
Now, it is apparent from the previous equation that there is no discontinuity in 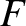 across the separatrix. Thus, given that
across the separatrix. Thus, given that
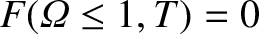 , it follows that
, it follows that
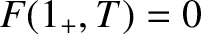 . It is also clear from Equations (11.105), (11.109), and (11.113) that
. It is also clear from Equations (11.105), (11.109), and (11.113) that
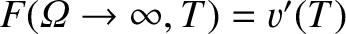 .
Thus, we can write
.
Thus, we can write
![\begin{displaymath}F({\mit\Omega},T)=v'(T)\left\{
\begin{array}{llr}
0&&-1\leq {...
...x]
{\cal F}({\mit\Omega})&~~&{\mit\Omega}>1
\end{array}\right.,\end{displaymath}](img3589.png) |
(11.136) |
where
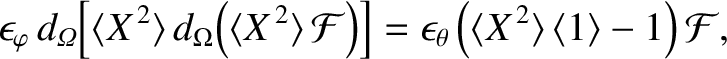 |
(11.137) |
and
Here,
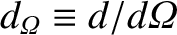 .
.
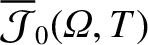 ,
,
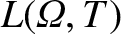 , and
, and
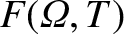 .
In order to determine the forms of these functions, we need to expand our model to higher order. (See Section 8.8.)
.
In order to determine the forms of these functions, we need to expand our model to higher order. (See Section 8.8.)
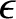 , we obtain
we obtain
, we obtain
we obtain
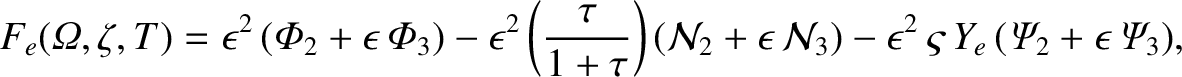
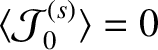 , by symmetry.
Hence,
where use has been made of Equation (11.116).
, by symmetry.
Hence,
where use has been made of Equation (11.116).
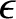 ,
we obtain
,
we obtain
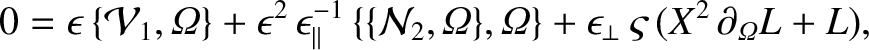
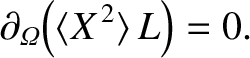
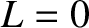 within the island separatrix.
Note that
within the island separatrix.
Note that
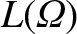 is discontinuous across the island separatrix, which implies that the pressure gradient is also discontinuous across the separatrix. As discussed in Section 8.9, we expect this discontinuity to be resolved in a layer of characteristic thickness
is discontinuous across the island separatrix, which implies that the pressure gradient is also discontinuous across the separatrix. As discussed in Section 8.9, we expect this discontinuity to be resolved in a layer of characteristic thickness 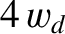 on the separatrix [see Equation (8.84) and Table 8.1].
on the separatrix [see Equation (8.84) and Table 8.1].
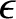 , we obtain
we obtain
, we obtain
we obtain
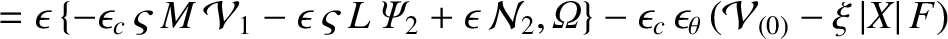
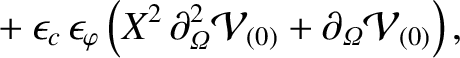
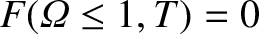 , we get
, we get
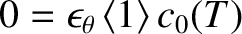
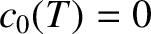 . Hence, given that we have already concluded that
. Hence, given that we have already concluded that 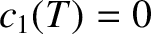 , Equations (11.121) and
(11.122) yield
, Equations (11.121) and
(11.122) yield
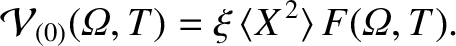
![$\displaystyle \epsilon_\varphi\,\partial_{\mit\Omega}\!\left[\langle X^{\,2}\ra...
...ht] = \epsilon_\theta\left(\langle X^{\,2}\rangle\,\langle 1\rangle -1\right)F.$](img3585.png)
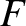 across the separatrix. Thus, given that
across the separatrix. Thus, given that
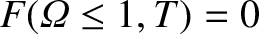 , it follows that
, it follows that
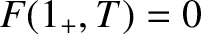 . It is also clear from Equations (11.105), (11.109), and (11.113) that
. It is also clear from Equations (11.105), (11.109), and (11.113) that
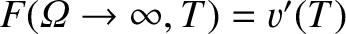 .
Thus, we can write
where
and
Here,
.
Thus, we can write
where
and
Here,
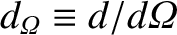 .
.