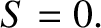For certain values of 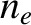 ,
, 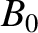 , and
, and 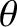 , the wave refractive index,
, the wave refractive index,  , is zero.
For other values, the refractive index is infinite. In both cases (assuming that
, is zero.
For other values, the refractive index is infinite. In both cases (assuming that  is a slowly varying function of position), a transition is made from a region
in which the wave in question propagates to a region in which the wave decays, or vice versa.
It is demonstrated in Section 6.3 that wave reflection occurs
at those points where
is a slowly varying function of position), a transition is made from a region
in which the wave in question propagates to a region in which the wave decays, or vice versa.
It is demonstrated in Section 6.3 that wave reflection occurs
at those points where  is zero, and in Section 6.4 that wave absorption occurs at those points
where
is zero, and in Section 6.4 that wave absorption occurs at those points
where  is infinite. The former points are called
wave cutoffs, whereas the latter are termed wave resonances.
is infinite. The former points are called
wave cutoffs, whereas the latter are termed wave resonances.
According to Equations (5.44) and (5.45)–(5.47), cutoff occurs when
 |
(5.61) |
or
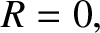 |
(5.62) |
or
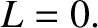 |
(5.63) |
The cutoff points are independent of the direction of
propagation of the wave relative to the magnetic field.
According to Equation (5.50), resonance takes place when
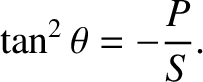 |
(5.64) |
Evidently, resonance points do depend on the direction of propagation
of the wave relative to the magnetic field. For the case of
parallel propagation, resonance occurs whenever
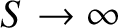 .
In other words, when
.
In other words, when
 |
(5.65) |
or
 |
(5.66) |
For the case of perpendicular propagation, resonance occurs
when
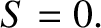 |
(5.67) |
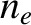 ,
, 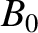 , and
, and 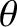 , the wave refractive index,
, the wave refractive index,  , is zero.
For other values, the refractive index is infinite. In both cases (assuming that
, is zero.
For other values, the refractive index is infinite. In both cases (assuming that  is a slowly varying function of position), a transition is made from a region
in which the wave in question propagates to a region in which the wave decays, or vice versa.
It is demonstrated in Section 6.3 that wave reflection occurs
at those points where
is a slowly varying function of position), a transition is made from a region
in which the wave in question propagates to a region in which the wave decays, or vice versa.
It is demonstrated in Section 6.3 that wave reflection occurs
at those points where  is zero, and in Section 6.4 that wave absorption occurs at those points
where
is zero, and in Section 6.4 that wave absorption occurs at those points
where  is infinite. The former points are called
wave cutoffs, whereas the latter are termed wave resonances.
is infinite. The former points are called
wave cutoffs, whereas the latter are termed wave resonances.

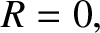
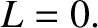
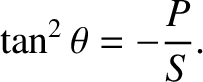
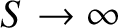 .
In other words, when
.
In other words, when