Next: Resonances Up: Waves in Inhomogeneous Plasmas Previous: WKB Solutions Contents
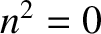 , or a resonance, where
, or a resonance, where
 . Let us
now examine what happens to electromagnetic waves propagating through
a plasma when they encounter a cutoff or a resonance.
. Let us
now examine what happens to electromagnetic waves propagating through
a plasma when they encounter a cutoff or a resonance.
Suppose that a cutoff is located at 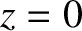 , so that
, so that
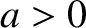 . It is evident, from the
WKB solutions, (6.17) and (6.18), that
the cutoff point lies at the boundary between a region (
. It is evident, from the
WKB solutions, (6.17) and (6.18), that
the cutoff point lies at the boundary between a region (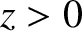 ) in which
electromagnetic
waves propagate, and a region (
) in which
electromagnetic
waves propagate, and a region (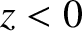 ) in which the waves are evanescent.
In a physically realistic solution, we would expect the wave amplitude to
decay (as
) in which the waves are evanescent.
In a physically realistic solution, we would expect the wave amplitude to
decay (as  decreases) in the evanescent region
decreases) in the evanescent region 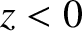 . Let us search for
such a wave solution.
. Let us search for
such a wave solution.
In the immediate vicinity of the cutoff point,
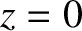 , Equations (6.3) and (6.19) yield
, Equations (6.3) and (6.19) yield
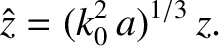 |
(6.21) |
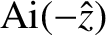 and
and
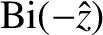 (Abramowitz and Stegun 1965).
(Abramowitz and Stegun 1965).
The second solution,
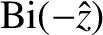 ,
is unphysical, because it blows up as
,
is unphysical, because it blows up as
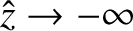 .
The physical solution,
.
The physical solution,
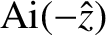 , has the asymptotic
behavior
, has the asymptotic
behavior
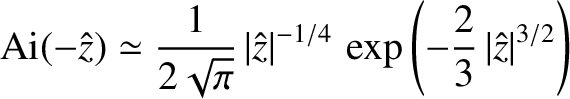 |
(6.22) |
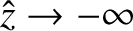 , and
, and
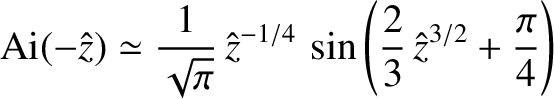 |
(6.23) |
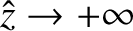 .
.
Suppose that a unit amplitude plane electromagnetic wave, polarized in the
 -direction, is launched
from an antenna, located at large positive
-direction, is launched
from an antenna, located at large positive  , toward the cutoff point at
, toward the cutoff point at 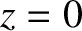 .
It is assumed that
.
It is assumed that 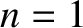 at the launch point.
In the non-evanescent region,
at the launch point.
In the non-evanescent region, 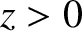 , the wave can be
represented as a linear combination
of propagating WKB solutions:
, the wave can be
represented as a linear combination
of propagating WKB solutions:
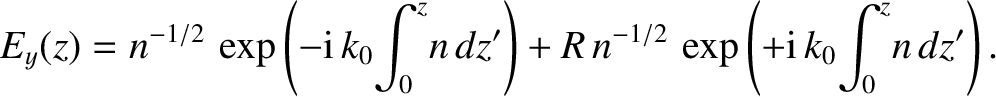 |
(6.24) |
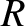 is the coefficient of reflection.
In the vicinity of the cutoff point (i.e.,
is the coefficient of reflection.
In the vicinity of the cutoff point (i.e.,  small and positive,
which corresponds to
small and positive,
which corresponds to 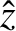 large and positive),
the previous expression reduces to
However, we have another expression for the wave in this region:
large and positive),
the previous expression reduces to
However, we have another expression for the wave in this region:
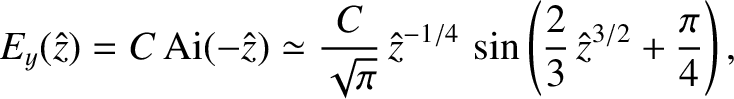 |
(6.26) |
 is an arbitrary constant.
The previous equation can be written
A comparison of Equations (6.25) and (6.27) reveals that
is an arbitrary constant.
The previous equation can be written
A comparison of Equations (6.25) and (6.27) reveals that
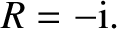 |
(6.28) |
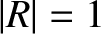 ) with a
) with a  phase-shift.
phase-shift.