Next: Resonant Layers Up: Waves in Inhomogeneous Plasmas Previous: Cutoffs Contents
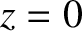 , so that
in the immediate vicinity of this point, where
, so that
in the immediate vicinity of this point, where 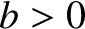 . Here,
. Here, 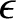 is a small real constant. We introduce
is a small real constant. We introduce 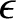 in our analysis principally
as a mathematical artifice to ensure that
in our analysis principally
as a mathematical artifice to ensure that 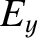 remains single-valued and
finite. However, as will become clear later on,
remains single-valued and
finite. However, as will become clear later on, 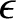 has a physical significance
in terms of the damping or the spontaneous excitation of waves.
has a physical significance
in terms of the damping or the spontaneous excitation of waves.
In the immediate vicinity of the resonance point,  , Equations (6.3) and (6.29)
yield
, Equations (6.3) and (6.29)
yield
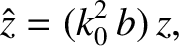 |
(6.31) |
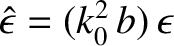 . This equation is
singular at the point
. This equation is
singular at the point
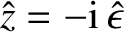 .
Thus, it is necessary to
introduce a branch-cut into the complex-
.
Thus, it is necessary to
introduce a branch-cut into the complex-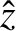 plane, so as to
ensure that
plane, so as to
ensure that
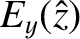 is single-valued. If
is single-valued. If
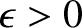 then the
branch-cut lies in the lower half-plane, whereas if
then the
branch-cut lies in the lower half-plane, whereas if
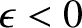 then
the branch-cut lies in the upper half-plane. (See Figure 6.1.) Suppose that the
argument of
then
the branch-cut lies in the upper half-plane. (See Figure 6.1.) Suppose that the
argument of  is 0 on the positive real
is 0 on the positive real  -axis.
It follows that the argument of
-axis.
It follows that the argument of 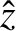 on the negative real
on the negative real 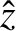 -axis
is
-axis
is 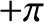 when
when
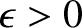 , and
, and 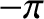 when
when
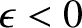 .
.
Let
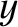 |
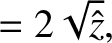 |
(6.32) |
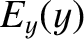 |
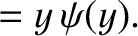 |
(6.33) |
 , Equation (6.30) transforms into
, Equation (6.30) transforms into
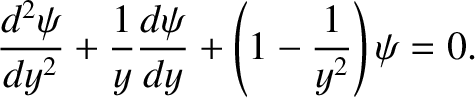 |
(6.34) |
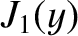 and
and 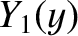 ,
respectively. Thus, on the positive real
,
respectively. Thus, on the positive real 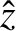 -axis, we can write
the most general solution to Equation (6.30) in the form
where
-axis, we can write
the most general solution to Equation (6.30) in the form
where 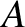 and
and 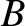 are two arbitrary constants.
are two arbitrary constants.
Let
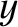 |
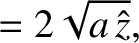 |
(6.36) |
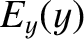 |
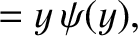 |
(6.37) |
![$\displaystyle a = \exp\left[-{\rm i}\,\pi\,{\rm sgn}(\epsilon)\right].$](img1992.png) |
(6.38) |
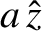 is zero on the negative real
is zero on the negative real
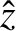 -axis.
In the limit
-axis.
In the limit
 , Equation (6.30) transforms into
, Equation (6.30) transforms into
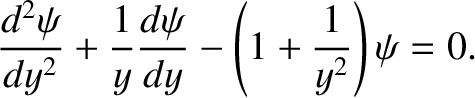 |
(6.39) |
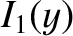 and
and 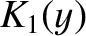 ,
respectively. Thus, on the negative real
,
respectively. Thus, on the negative real 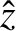 -axis, we can write
the most general solution to Equation (6.30) in the form
where
-axis, we can write
the most general solution to Equation (6.30) in the form
where  and
and 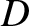 are two arbitrary constants.
are two arbitrary constants.
The Bessel functions 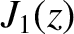 ,
, 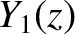 ,
, 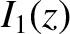 , and
, and 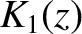 are all perfectly
well-defined (i.e., analytic) for
complex arguments, so the two expressions (6.35) and (6.40) must, in fact, be
identical.
In particular, the constants
are all perfectly
well-defined (i.e., analytic) for
complex arguments, so the two expressions (6.35) and (6.40) must, in fact, be
identical.
In particular, the constants  and
and 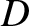 must somehow be related to the
constants
must somehow be related to the
constants 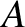 and
and 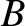 . In order to establish this relationship, it
is convenient to investigate the behavior of the expressions
(6.35) and (6.40) in the limit of small
. In order to establish this relationship, it
is convenient to investigate the behavior of the expressions
(6.35) and (6.40) in the limit of small 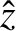 : that is,
: that is,
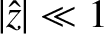 .
In this limit,
.
In this limit,
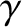 is Euler's constant (Abramowitz and Stegun 1965), and
is Euler's constant (Abramowitz and Stegun 1965), and 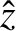 is assumed to lie on the positive
real
is assumed to lie on the positive
real 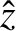 -axis. It follows, by a comparison of Equations (6.35), (6.40),
and (6.41)–(6.44), that the choice
-axis. It follows, by a comparison of Equations (6.35), (6.40),
and (6.41)–(6.44), that the choice
 |
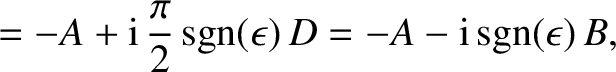 |
(6.45) |
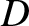 |
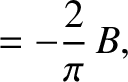 |
(6.46) |
In the limit
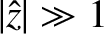 ,
,
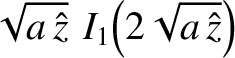 |
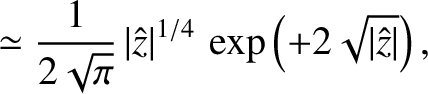 |
(6.47) |
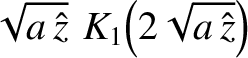 |
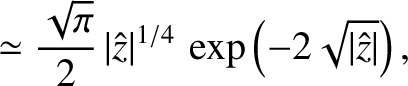 |
(6.48) |
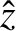 is assumed to lie on the negative real
is assumed to lie on the negative real 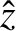 -axis.
It is clear that the
-axis.
It is clear that the 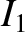 solution is unphysical, because it blows up
in the evanescent region
solution is unphysical, because it blows up
in the evanescent region
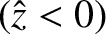 . Thus, the coefficient
. Thus, the coefficient  in expression
(6.40) must be set to zero in order to prevent
in expression
(6.40) must be set to zero in order to prevent
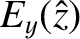 from
blowing up as
from
blowing up as
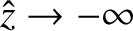 . According to Equation (6.45),
this constraint implies that
. According to Equation (6.45),
this constraint implies that
In the limit
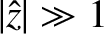 ,
,
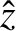 is assumed to lie on the positive real
is assumed to lie on the positive real 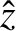 -axis.
It follows from Equations (6.35), (6.49), (6.50), and (6.51) that, in the
non-evanescent region (
-axis.
It follows from Equations (6.35), (6.49), (6.50), and (6.51) that, in the
non-evanescent region (
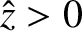 ), the most general
physical solution takes the form
where
), the most general
physical solution takes the form
where 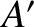 is an arbitrary constant.
is an arbitrary constant.
Suppose that a plane electromagnetic wave, polarized in the
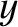 -direction, is launched
from an antenna, located at large positive
-direction, is launched
from an antenna, located at large positive 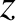 , toward the resonance
point at
, toward the resonance
point at 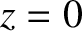 .
It is assumed that
.
It is assumed that 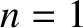 at the launch point.
In the non-evanescent region,
at the launch point.
In the non-evanescent region, 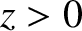 , the wave can be
represented as a linear combination
of propagating WKB solutions:
, the wave can be
represented as a linear combination
of propagating WKB solutions:
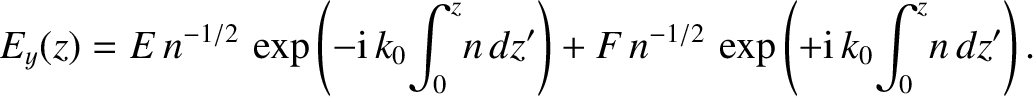 |
(6.53) |
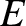 is the amplitude of the incident wave, and
is the amplitude of the incident wave, and 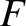 is the amplitude of
the reflected wave.
In the vicinity of the resonance point (i.e.,
is the amplitude of
the reflected wave.
In the vicinity of the resonance point (i.e., 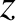 small and positive,
which corresponds to
small and positive,
which corresponds to 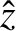 large and positive),
the previous expression reduces to
A comparison of Equations (6.52) and (6.54) shows that if
large and positive),
the previous expression reduces to
A comparison of Equations (6.52) and (6.54) shows that if
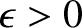 then
then
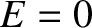 . In other words, there is a reflected wave, but no incident wave.
This corresponds to the spontaneous excitation of waves in the vicinity of the
resonance. On the other hand, if
. In other words, there is a reflected wave, but no incident wave.
This corresponds to the spontaneous excitation of waves in the vicinity of the
resonance. On the other hand, if
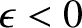 then
then 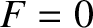 . In other words,
there is an incident wave, but no reflected wave. This corresponds to the
total absorption of incident waves in the vicinity of the resonance.
It is clear that if
. In other words,
there is an incident wave, but no reflected wave. This corresponds to the
total absorption of incident waves in the vicinity of the resonance.
It is clear that if
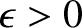 then
then 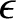 represents some sort of
spontaneous wave excitation mechanism, whereas if
represents some sort of
spontaneous wave excitation mechanism, whereas if
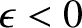 then
then
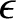 represents a wave absorption, or damping, mechanism.
We would normally expect plasmas to absorb incident wave energy, rather
than spontaneously emit waves, so we conclude that, under most circumstances,
represents a wave absorption, or damping, mechanism.
We would normally expect plasmas to absorb incident wave energy, rather
than spontaneously emit waves, so we conclude that, under most circumstances,
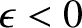 , and resonances absorb incident waves without reflection.
, and resonances absorb incident waves without reflection.