


Next: WKB Reflection Coefficient
Up: Wave Propagation in Inhomogeneous
Previous: WKB Solution as Asymptotic
We have seen that the differential equation
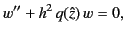 |
(1173) |
where
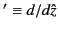 ,
possesses approximate WKB solutions of the form
,
possesses approximate WKB solutions of the form
Here, we have adopted an arbitrary phase reference level 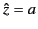 . The convenient
notation
. The convenient
notation
 is fairly self explanatory:
is fairly self explanatory:  and
and 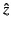 refer to the lower and
upper bounds of integration, respectively,
inside the exponential. It follows
that the other WKB solution can be written
refer to the lower and
upper bounds of integration, respectively,
inside the exponential. It follows
that the other WKB solution can be written
 (because we can reverse the limits
of integration inside the exponential to obtain minus the integral in
(because we can reverse the limits
of integration inside the exponential to obtain minus the integral in 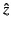 from
from 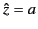 to
to
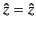 ).
).
Up to now, we have thought of 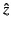 as a real variable representing
scaled height in the ionosphere. Let us now generalize our analysis somewhat,
and think of
as a real variable representing
scaled height in the ionosphere. Let us now generalize our analysis somewhat,
and think of 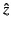 as a complex variable. There is nothing in our
derivation of the WKB solutions that depends crucially on
as a complex variable. There is nothing in our
derivation of the WKB solutions that depends crucially on 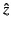 being a real variable, so we expect these solutions to remain valid when
being a real variable, so we expect these solutions to remain valid when
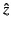 is reinterpreted as a complex variable. Incidentally, we must now
interpret
is reinterpreted as a complex variable. Incidentally, we must now
interpret
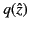 as some well-behaved function of the complex variable.
An approximate general solution of the differential equation (1175) in the
complex
as some well-behaved function of the complex variable.
An approximate general solution of the differential equation (1175) in the
complex 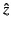 -plane can be written as as a linear superposition of the
two WKB solutions (1176)-(1177).
-plane can be written as as a linear superposition of the
two WKB solutions (1176)-(1177).
The parameter 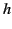 is
assumed to be much larger than unity.
It is clear from Equations (1176)-(1177) that
in some regions of the complex plane one of the WKB solutions is going to
be exponentially larger than the other. In such regions, it is not mathematically
consistent to retain the smaller WKB solution in the expression
for the general solution, because
the contribution of the smaller WKB solution is less than the intrinsic error
associated with the larger solution. Adopting the terminology
introduced in Section 8.13, the larger WKB solution is said to be
dominant, and
the smaller solution is said to be subdominant. Let us denote the
WKB solution (1176) as
is
assumed to be much larger than unity.
It is clear from Equations (1176)-(1177) that
in some regions of the complex plane one of the WKB solutions is going to
be exponentially larger than the other. In such regions, it is not mathematically
consistent to retain the smaller WKB solution in the expression
for the general solution, because
the contribution of the smaller WKB solution is less than the intrinsic error
associated with the larger solution. Adopting the terminology
introduced in Section 8.13, the larger WKB solution is said to be
dominant, and
the smaller solution is said to be subdominant. Let us denote the
WKB solution (1176) as
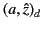 in regions of the
complex plane where it is dominant, and as
in regions of the
complex plane where it is dominant, and as
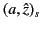 in regions
where it is subdominant. An analogous notation is adopted for the second
WKB solution (1177).
in regions
where it is subdominant. An analogous notation is adopted for the second
WKB solution (1177).
Suppose that
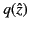 possesses a simple zero at the point
possesses a simple zero at the point
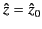 (chosen to be the origin, for the sake of convenience).
It follows that in the immediate neighborhood of the origin we can write
(chosen to be the origin, for the sake of convenience).
It follows that in the immediate neighborhood of the origin we can write
 |
(1176) |
where 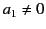 . It is convenient to adopt the origin as the
phase reference point (i.e.,
. It is convenient to adopt the origin as the
phase reference point (i.e.,  ), so the two WKB solutions become
), so the two WKB solutions become
 and
and
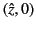 . We can define anti-Stokes lines in the
complex
. We can define anti-Stokes lines in the
complex 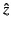 plane (see Section 8.13). These are lines that satisfy
plane (see Section 8.13). These are lines that satisfy
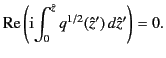 |
(1177) |
As we cross an anti-Stokes line, a dominant WKB solution becomes subdominant, and
vice versa. Thus,
 and
and
 . In the immediate
vicinity of an anti-Stokes line the two WKB solutions have about the same magnitude, so it is mathematically consistent to include the contributions from
both solutions in the expression for the general solution.
In such a region, we can drop the subscripts
. In the immediate
vicinity of an anti-Stokes line the two WKB solutions have about the same magnitude, so it is mathematically consistent to include the contributions from
both solutions in the expression for the general solution.
In such a region, we can drop the subscripts 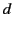 and
and 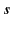 , because the WKB
solutions are neither
dominant nor subdominant, and write the WKB solutions simply as
, because the WKB
solutions are neither
dominant nor subdominant, and write the WKB solutions simply as
 and
and
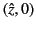 .
.
It is clear from Equations (1176)-(1177) that the WKB solutions are not single-valued functions of 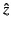 , because they depend on
, because they depend on
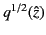 , which is a
double-valued function. Thus, if we wish to write an approximate
analytic solution
to the differential equation (1175) then we cannot express
this solution as the same linear combination of WKB solutions in all
regions of the complex
, which is a
double-valued function. Thus, if we wish to write an approximate
analytic solution
to the differential equation (1175) then we cannot express
this solution as the same linear combination of WKB solutions in all
regions of the complex 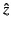 -plane. This implies that there must exist
certain lines in the complex
-plane. This implies that there must exist
certain lines in the complex 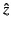 -plane across which the mix of WKB
solutions in our expression for
the general solution changes discontinuously.
These
lines are called Stokes lines (see Section 8.13), and satisfy
-plane across which the mix of WKB
solutions in our expression for
the general solution changes discontinuously.
These
lines are called Stokes lines (see Section 8.13), and satisfy
 |
(1178) |
As we cross a Stokes line, the coefficient of the dominant
WKB solution
in our expression for the general solution must
remain unchanged, but the coefficient of the subdominant
solution is allowed to change discontinuously. Incidentally,
this is
perfectly consistent with the fact that the
general solution is analytic: the
jump in our expression for the general
solution due to the jump in the coefficient of the subdominant
WKB solution is less than the intrinsic error in this expression
due to the intrinsic error in the dominant WKB solution. Once we appreciate
that the coefficient of the subdominant solution can only change at a Stokes
line, we can retain both WKB solutions in our expression for the general
solution throughout the complex 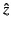 -plane. In practice, we can only see a
subdominant solution in the immediate vicinity of an anti-Stokes line, but
if we were to evaluate the WKB solutions to higher accuracy [i.e.,
by retaining more terms in the asymptotic series in Equations (1176)-(1177)] then we could, in principle,
follow a subdominant solution all the way to a neighboring Stokes line.
-plane. In practice, we can only see a
subdominant solution in the immediate vicinity of an anti-Stokes line, but
if we were to evaluate the WKB solutions to higher accuracy [i.e.,
by retaining more terms in the asymptotic series in Equations (1176)-(1177)] then we could, in principle,
follow a subdominant solution all the way to a neighboring Stokes line.
In the immediate vicinity of the origin
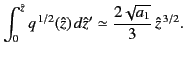 |
(1179) |
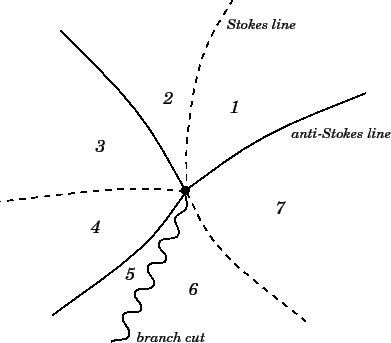
It follows from Equations (1179) and (1180) that three Stokes lines and
three anti-Stokes lines radiate from a zero of
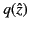 . The general
arrangement of Stokes and anti-Stokes lines in the vicinity of a
. The general
arrangement of Stokes and anti-Stokes lines in the vicinity of a  point
is sketched in Figure 23. Note that a branch cut must also radiate from the
point
is sketched in Figure 23. Note that a branch cut must also radiate from the
 point in order to uniquely specify the function
point in order to uniquely specify the function
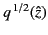 .
Thus, in general, seven lines radiate from a zero of
.
Thus, in general, seven lines radiate from a zero of
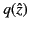 ,
dividing the complex
,
dividing the complex 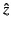 plane into seven domains (numbered 1 through 7).
plane into seven domains (numbered 1 through 7).
Figure:
The
arrangement of Stokes lines (dashed) and anti-Stokes lines
(solid) around a simple zero of
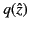 . Also shown is the branch
cut (wavy line). All of the lines radiate from the point
. Also shown is the branch
cut (wavy line). All of the lines radiate from the point  .
.
 |
Let us write our general solution as
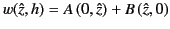 |
(1180) |
on the anti-Stokes line between domains 1 and 7, where  and
and
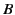 are arbitrary constants. Suppose that the WKB
solution
are arbitrary constants. Suppose that the WKB
solution
 is dominant in domain 7. Thus, in domain 7 the general
solution takes the form
is dominant in domain 7. Thus, in domain 7 the general
solution takes the form
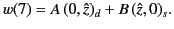 |
(1181) |
Let us move into domain 1. In doing so, we cross an anti-Stokes line, so
the dominant solution becomes subdominant, and vice versa. Thus,
in domain 1, the general solution takes the form
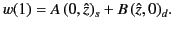 |
(1182) |
Let us now move into domain 2. In doing so, we cross a Stokes line, so the
coefficient of the dominant solution, 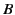 , must remain constant, but the
coefficient of the subdominant solution,
, must remain constant, but the
coefficient of the subdominant solution,  , is allowed to change.
Suppose that the coefficient of the subdominant solution jumps by
, is allowed to change.
Suppose that the coefficient of the subdominant solution jumps by
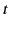 times the coefficient of the dominant solution, where
times the coefficient of the dominant solution, where 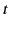 is an undetermined
constant. It follows that in domain 2 the general solution takes the form
is an undetermined
constant. It follows that in domain 2 the general solution takes the form
 |
(1183) |
Let us now move into domain 3. In doing so, we cross an anti-Stokes line,
so the
the dominant solution becomes subdominant, and vice versa. Thus,
in domain 3, the general solution takes the form
 |
(1184) |
Let us now move into domain 4. In doing so, we cross a Stokes line, so the
coefficient of the dominant solution must remain constant, but the
coefficient of the subdominant solution is allowed to change.
Suppose that the coefficient of the subdominant solution jumps by
 times the coefficient of the dominant solution, where
times the coefficient of the dominant solution, where  is an undetermined
constant. It follows that in domain 4 the general solution takes the form
is an undetermined
constant. It follows that in domain 4 the general solution takes the form
![$\displaystyle w(4) =( A+t\,B)\,(0,\hat{z})_d + (B+ u\,[A+t\,B])\,(\hat{z},0)_s.$](img2502.png) |
(1185) |
Let us now move into domain 5. In doing so, we cross an anti-Stokes line,
so the
the dominant solution becomes subdominant, and vice versa. Thus,
in domain 5 the general solution takes the form
![$\displaystyle w(5) =( A+t\,B)\,(0,\hat{z})_s + (B+ u\,[A+t\,B])\,(\hat{z},0)_d.$](img2503.png) |
(1186) |
Let us now move into domain 6. In doing so, we cross the branch cut in an anti-clockwise
direction. Thus, the argument of 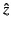 decreases by
decreases by 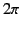 . It follows
from Equation (1178) that
. It follows
from Equation (1178) that
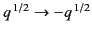 and
and
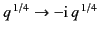 . The following rules for tracing the WKB solutions
across the branch cut (in an anti-clockwise direction) ensure that the
general solution is continuous across the cut [see Equations (1176)-(1177)]:
. The following rules for tracing the WKB solutions
across the branch cut (in an anti-clockwise direction) ensure that the
general solution is continuous across the cut [see Equations (1176)-(1177)]:
Note that the properties of dominancy and subdominancy are preserved when the
branch cut is crossed. It follows that in domain 6 the general solution
takes the form
![$\displaystyle w(6) =-{\rm i}\,( A+t\,B)\,(\hat{z},0)_s -{\rm i}\,(B+ u\,[A+t\,B])\,(0,\hat{z})_d.$](img2511.png) |
(1189) |
Let us, finally, move into domain 7. In doing so, we cross a Stokes line, so the
coefficient of the dominant solution must remain constant, but the
coefficient of the subdominant solution is allowed to change.
Suppose that the coefficient of the subdominant solution jumps by
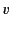 times the coefficient of the dominant solution, where
times the coefficient of the dominant solution, where 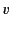 is an undetermined
constant. It follows that in domain 7 the general solution takes the form
is an undetermined
constant. It follows that in domain 7 the general solution takes the form
![$\displaystyle w(7) =-{\rm i}\,( A+t\,B +v\,\{B+ u\,[A+t\,B]\}) \,(\hat{z},0)_s -{\rm i}\,(B+ u\,[A+t\,B])\,(0,\hat{z})_d.$](img2512.png) |
(1190) |
Now, we expect our general solution to be an analytic function, so it follows
that the solutions (1183) and (1192) must be identical. Thus, we can compare
the coefficients of the two WKB solutions,
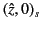 and
and
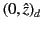 . Because
. Because  and
and 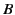 are arbitrary, we can also compare the coefficients
of
are arbitrary, we can also compare the coefficients
of  and
and 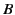 . Comparing the coefficients of
. Comparing the coefficients of
 ,
we find
,
we find
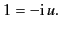 |
(1191) |
Comparing the coefficients of
 yields
yields
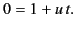 |
(1192) |
Comparing the coefficients of
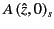 gives
gives
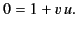 |
(1193) |
Finally, comparing the coefficients of
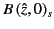 yields
yields
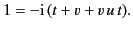 |
(1194) |
Equations (1193)-(1196) imply that
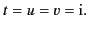 |
(1195) |
In other words, if we adopt the simple rule that every time we cross a
Stokes line in an anti-clockwise direction the coefficient of the
subdominant solution jumps by  times the coefficient of the
dominant solution then this ensures that our expression for the
general solution, (1182), behaves as an analytic function. Here, the constant
times the coefficient of the
dominant solution then this ensures that our expression for the
general solution, (1182), behaves as an analytic function. Here, the constant
 is usually called a Stokes constant. Note that if we cross a
Stokes line in a clockwise direction then the coefficient of the
subdominant solution has to jump by
is usually called a Stokes constant. Note that if we cross a
Stokes line in a clockwise direction then the coefficient of the
subdominant solution has to jump by  times the coefficient of
the dominant solution in order to ensure that our general solution behaves
as an analytic function.
times the coefficient of
the dominant solution in order to ensure that our general solution behaves
as an analytic function.



Next: WKB Reflection Coefficient
Up: Wave Propagation in Inhomogeneous
Previous: WKB Solution as Asymptotic
Richard Fitzpatrick
2014-06-27
![]() as a real variable representing
scaled height in the ionosphere. Let us now generalize our analysis somewhat,
and think of
as a real variable representing
scaled height in the ionosphere. Let us now generalize our analysis somewhat,
and think of ![]() as a complex variable. There is nothing in our
derivation of the WKB solutions that depends crucially on
as a complex variable. There is nothing in our
derivation of the WKB solutions that depends crucially on ![]() being a real variable, so we expect these solutions to remain valid when
being a real variable, so we expect these solutions to remain valid when
![]() is reinterpreted as a complex variable. Incidentally, we must now
interpret
is reinterpreted as a complex variable. Incidentally, we must now
interpret
![]() as some well-behaved function of the complex variable.
An approximate general solution of the differential equation (1175) in the
complex
as some well-behaved function of the complex variable.
An approximate general solution of the differential equation (1175) in the
complex ![]() -plane can be written as as a linear superposition of the
two WKB solutions (1176)-(1177).
-plane can be written as as a linear superposition of the
two WKB solutions (1176)-(1177).
![]() is
assumed to be much larger than unity.
It is clear from Equations (1176)-(1177) that
in some regions of the complex plane one of the WKB solutions is going to
be exponentially larger than the other. In such regions, it is not mathematically
consistent to retain the smaller WKB solution in the expression
for the general solution, because
the contribution of the smaller WKB solution is less than the intrinsic error
associated with the larger solution. Adopting the terminology
introduced in Section 8.13, the larger WKB solution is said to be
dominant, and
the smaller solution is said to be subdominant. Let us denote the
WKB solution (1176) as
is
assumed to be much larger than unity.
It is clear from Equations (1176)-(1177) that
in some regions of the complex plane one of the WKB solutions is going to
be exponentially larger than the other. In such regions, it is not mathematically
consistent to retain the smaller WKB solution in the expression
for the general solution, because
the contribution of the smaller WKB solution is less than the intrinsic error
associated with the larger solution. Adopting the terminology
introduced in Section 8.13, the larger WKB solution is said to be
dominant, and
the smaller solution is said to be subdominant. Let us denote the
WKB solution (1176) as
![]() in regions of the
complex plane where it is dominant, and as
in regions of the
complex plane where it is dominant, and as
![]() in regions
where it is subdominant. An analogous notation is adopted for the second
WKB solution (1177).
in regions
where it is subdominant. An analogous notation is adopted for the second
WKB solution (1177).
![]() possesses a simple zero at the point
possesses a simple zero at the point
![]() (chosen to be the origin, for the sake of convenience).
It follows that in the immediate neighborhood of the origin we can write
(chosen to be the origin, for the sake of convenience).
It follows that in the immediate neighborhood of the origin we can write
![]() , because they depend on
, because they depend on
![]() , which is a
double-valued function. Thus, if we wish to write an approximate
analytic solution
to the differential equation (1175) then we cannot express
this solution as the same linear combination of WKB solutions in all
regions of the complex
, which is a
double-valued function. Thus, if we wish to write an approximate
analytic solution
to the differential equation (1175) then we cannot express
this solution as the same linear combination of WKB solutions in all
regions of the complex ![]() -plane. This implies that there must exist
certain lines in the complex
-plane. This implies that there must exist
certain lines in the complex ![]() -plane across which the mix of WKB
solutions in our expression for
the general solution changes discontinuously.
These
lines are called Stokes lines (see Section 8.13), and satisfy
-plane across which the mix of WKB
solutions in our expression for
the general solution changes discontinuously.
These
lines are called Stokes lines (see Section 8.13), and satisfy
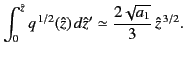

![]() and
and
![]() . Because
. Because ![]() and
and ![]() are arbitrary, we can also compare the coefficients
of
are arbitrary, we can also compare the coefficients
of ![]() and
and ![]() . Comparing the coefficients of
. Comparing the coefficients of
![]() ,
we find
,
we find