


Next: Anomalous Dispersion and Resonant
Up: Wave Propagation in Uniform
Previous: Introduction
Consider an electromagnetic wave propagating
through a transparent, isotropic, dielectric medium.
The electric displacement inside the medium is given by
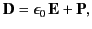 |
(776) |
where 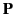 is the electric
polarization. Because electrons are much lighter than
ions (or atomic nuclei),
we would expect the former to displace further than the latter under
the influence of an electric field. Thus, to a first
approximation, the polarization,
is the electric
polarization. Because electrons are much lighter than
ions (or atomic nuclei),
we would expect the former to displace further than the latter under
the influence of an electric field. Thus, to a first
approximation, the polarization, 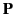 , is determined by the electron
response to the wave. Suppose that the electrons displace an average distance
, is determined by the electron
response to the wave. Suppose that the electrons displace an average distance
 from their rest positions in the presence of the wave. It follows
that
from their rest positions in the presence of the wave. It follows
that
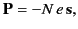 |
(777) |
where 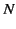 is the number density of electrons, and
is the number density of electrons, and 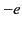 the electron charge.
the electron charge.
Let us assume that the electrons are bound ``quasi-elastically'' to
their rest positions, so that they seek to return to these positions
when displaced from them by an electric field. It follows that  satisfies a differential equation of the form
satisfies a differential equation of the form
 |
(778) |
where 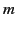 is the electron mass,
is the electron mass,
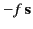 is the restoring force,
and
is the restoring force,
and 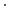 denotes a partial derivative with respect to time.
The previous equation can also be written
denotes a partial derivative with respect to time.
The previous equation can also be written
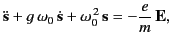 |
(779) |
where
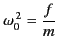 |
(780) |
is the characteristic oscillation
frequency of the electrons. In almost all dielectric
media, this frequency lies in the far ultraviolet region of the
electromagnetic spectrum. Note that we have added a phenomenological
damping term,
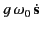 , to Equation (780), in order to take into account the
fact that an electron excited by an impulsive electric field does not
oscillate for ever. In fact, electrons in dielectric media
act like high-Q oscillators, which is another way of
saying that the dimensionless damping constant,
, to Equation (780), in order to take into account the
fact that an electron excited by an impulsive electric field does not
oscillate for ever. In fact, electrons in dielectric media
act like high-Q oscillators, which is another way of
saying that the dimensionless damping constant, 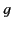 , is typically much less than
unity. Thus, an electron in a dielectric medium ``rings'' for a long time after being excited by an electromagnetic
impulse.
, is typically much less than
unity. Thus, an electron in a dielectric medium ``rings'' for a long time after being excited by an electromagnetic
impulse.
Let us assume that the electrons oscillate in sympathy with the wave at the
wave frequency,  . It follows from Equation (780) that
. It follows from Equation (780) that
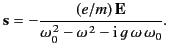 |
(781) |
Here, we have neglected the response of the electrons to the
magnetic component of the wave. It is easily demonstrated that this
is a good approximation provided the electrons do not oscillate with
relativistic velocities (i.e., provided the amplitude of
the wave is not too large--see Section 7.7).
Thus, Equation (778) yields
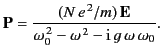 |
(782) |
Because, by definition,
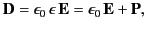 |
(783) |
it follows
that
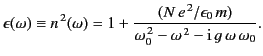 |
(784) |
Thus, the index of refraction is indeed frequency dependent. Because 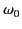 typically lies in the ultraviolet region of the spectrum (and
typically lies in the ultraviolet region of the spectrum (and
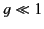 ), it is clear that the denominator,
), it is clear that the denominator,
 , is positive throughout the visible spectrum, and is
larger at the red than at the blue end of this spectrum. This implies that
blue light is refracted more strongly than red light. This state of affairs, in which higher frequency waves are refracted more strongly than
lower frequency waves, is termed normal
dispersion. Incidentally, an expression, like the previous one, that (effectively) specifies the
phase velocity of waves propagating through a dielectric medium, as a function of their frequency, is usually
called a dispersion relation.
, is positive throughout the visible spectrum, and is
larger at the red than at the blue end of this spectrum. This implies that
blue light is refracted more strongly than red light. This state of affairs, in which higher frequency waves are refracted more strongly than
lower frequency waves, is termed normal
dispersion. Incidentally, an expression, like the previous one, that (effectively) specifies the
phase velocity of waves propagating through a dielectric medium, as a function of their frequency, is usually
called a dispersion relation.
Let us now suppose that there are 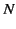 molecules per unit volume,
with
molecules per unit volume,
with 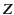 electrons per molecule, and that, instead of a single oscillation
frequency for all electrons, there are
electrons per molecule, and that, instead of a single oscillation
frequency for all electrons, there are  electrons per molecule with
oscillation frequency
electrons per molecule with
oscillation frequency 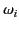 and damping constant
and damping constant 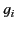 . It is
easily demonstrated that Equation (785) generalizes to give
. It is
easily demonstrated that Equation (785) generalizes to give
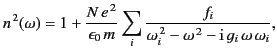 |
(785) |
where the oscillator strengths,  , satisfy the sum rule,
, satisfy the sum rule,
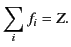 |
(786) |
A more exact quantum mechanical treatment of the response of an atom,
or molecule, to a low amplitude electromagnetic wave also leads to a
dispersion relation
of the previous form, except that the quantities
 ,
, 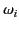 , and
, and 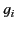 can, in principle,
be calculated exactly. In practice, this is too difficult, except
in very simple cases.
can, in principle,
be calculated exactly. In practice, this is too difficult, except
in very simple cases.
Because the damping constants, 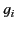 , are generally small compared to unity,
it follows from Equation (786) that
, are generally small compared to unity,
it follows from Equation (786) that  is a predominately real
quantity at most wave frequencies. The factor
is a predominately real
quantity at most wave frequencies. The factor
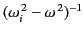 is positive for
is positive for
 , and negative for
, and negative for
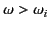 .
Thus, at low frequencies (i.e., below the smallest
.
Thus, at low frequencies (i.e., below the smallest 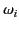 ) all of the terms
appearing in the sum on the right-hand side of (786) are positive, and
) all of the terms
appearing in the sum on the right-hand side of (786) are positive, and  is consequently
greater than unity. As
is consequently
greater than unity. As  is raised, such that
it exceeds successive
is raised, such that
it exceeds successive 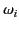 values, more and more negative terms occur
in
the sum, until eventually the whole sum is negative, and
values, more and more negative terms occur
in
the sum, until eventually the whole sum is negative, and  is less than unity. Hence, at very high frequencies, electromagnetic
waves propagate through dielectric media with phase velocities that exceed
the velocity of light in a vacuum. For
is less than unity. Hence, at very high frequencies, electromagnetic
waves propagate through dielectric media with phase velocities that exceed
the velocity of light in a vacuum. For
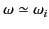 ,
Equation (786) predicts strong variation of the refractive index with
frequency. Let us examine this phenomenon more closely.
,
Equation (786) predicts strong variation of the refractive index with
frequency. Let us examine this phenomenon more closely.



Next: Anomalous Dispersion and Resonant
Up: Wave Propagation in Uniform
Previous: Introduction
Richard Fitzpatrick
2014-06-27
![]() satisfies a differential equation of the form
satisfies a differential equation of the form
![]() . It follows from Equation (780) that
. It follows from Equation (780) that
![]() molecules per unit volume,
with
molecules per unit volume,
with ![]() electrons per molecule, and that, instead of a single oscillation
frequency for all electrons, there are
electrons per molecule, and that, instead of a single oscillation
frequency for all electrons, there are ![]() electrons per molecule with
oscillation frequency
electrons per molecule with
oscillation frequency ![]() and damping constant
and damping constant ![]() . It is
easily demonstrated that Equation (785) generalizes to give
. It is
easily demonstrated that Equation (785) generalizes to give
![]() , are generally small compared to unity,
it follows from Equation (786) that
, are generally small compared to unity,
it follows from Equation (786) that ![]() is a predominately real
quantity at most wave frequencies. The factor
is a predominately real
quantity at most wave frequencies. The factor
![]() is positive for
is positive for
![]() , and negative for
, and negative for
![]() .
Thus, at low frequencies (i.e., below the smallest
.
Thus, at low frequencies (i.e., below the smallest ![]() ) all of the terms
appearing in the sum on the right-hand side of (786) are positive, and
) all of the terms
appearing in the sum on the right-hand side of (786) are positive, and ![]() is consequently
greater than unity. As
is consequently
greater than unity. As ![]() is raised, such that
it exceeds successive
is raised, such that
it exceeds successive ![]() values, more and more negative terms occur
in
the sum, until eventually the whole sum is negative, and
values, more and more negative terms occur
in
the sum, until eventually the whole sum is negative, and ![]() is less than unity. Hence, at very high frequencies, electromagnetic
waves propagate through dielectric media with phase velocities that exceed
the velocity of light in a vacuum. For
is less than unity. Hence, at very high frequencies, electromagnetic
waves propagate through dielectric media with phase velocities that exceed
the velocity of light in a vacuum. For
![]() ,
Equation (786) predicts strong variation of the refractive index with
frequency. Let us examine this phenomenon more closely.
,
Equation (786) predicts strong variation of the refractive index with
frequency. Let us examine this phenomenon more closely.