


Next: Ferromagnetism
Up: Magnetostatics in Magnetic Media
Previous: Magnetization
In a large class of materials, there exists an approximately linear
relationship between 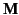 and
and  . If the material
is isotropic then
. If the material
is isotropic then
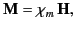 |
(690) |
where the dimensionless quantity 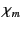 is known as the magnetic susceptibility. If
is known as the magnetic susceptibility. If 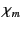 is
positive then the material is called paramagnetic, and the magnetic field
is strengthened by the presence of the material. If
is
positive then the material is called paramagnetic, and the magnetic field
is strengthened by the presence of the material. If 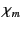 is
negative then the material is called diamagnetic, and the magnetic field
is weakened in the presence of the material. The magnetic
susceptibilities of paramagnetic and diamagnetic materials are
generally extremely small. A few sample values are given in Table 1.
is
negative then the material is called diamagnetic, and the magnetic field
is weakened in the presence of the material. The magnetic
susceptibilities of paramagnetic and diamagnetic materials are
generally extremely small. A few sample values are given in Table 1.
Table:
Magnetic susceptibilities of some paramagnetic and diamagnetic
materials at room temperature. Data obtained from the Handbook of Chemistry and Physics, Chemical Rubber Company Press, Baca Raton, FL.
| Material |
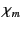
|
| |
|
| Aluminium |

|
| Copper |
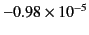
|
| Diamond |
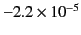
|
| Tungsten |
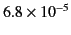
|
| Hydrogen (1 atm) |
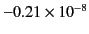
|
| Oxygen (1 atm) |

|
| Nitrogen (1 atm) |
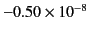
|
|
A linear relationship between 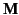 and
and  also
implies a linear relationship between
also
implies a linear relationship between 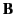 and
and  .
In fact, from Equation (689), we can write
.
In fact, from Equation (689), we can write
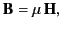 |
(691) |
where
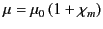 |
(692) |
is termed the magnetic permeability of the material
in question. (Likewise,
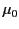 is termed the permeability of free space.) It is clear from
Table 1 that the permeabilities of common diamagnetic and paramagnetic
materials do not differ substantially from that of free space. In fact,
to all intents and purposes, the magnetic properties of such materials
can be safely neglected (i.e.,
is termed the permeability of free space.) It is clear from
Table 1 that the permeabilities of common diamagnetic and paramagnetic
materials do not differ substantially from that of free space. In fact,
to all intents and purposes, the magnetic properties of such materials
can be safely neglected (i.e.,
 ).
).



Next: Ferromagnetism
Up: Magnetostatics in Magnetic Media
Previous: Magnetization
Richard Fitzpatrick
2014-06-27
![]() and
and ![]() also
implies a linear relationship between
also
implies a linear relationship between ![]() and
and ![]() .
In fact, from Equation (689), we can write
.
In fact, from Equation (689), we can write