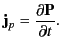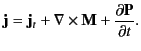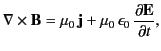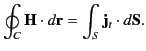Next: Magnetic Susceptibility and Permeability
Up: Magnetostatics in Magnetic Media
Previous: Magnetostatics in Magnetic Media
All matter is built up out of atoms, and every atom contains moving electrons. The currents
associated with these electrons
are termed atomic currents. Each atomic current is
a tiny closed circuit of atomic dimensions, and may therefore be
appropriately described as a magnetic dipole. If the atomic currents
of a given atom all flow in the same plane then the atomic dipole moment is directed normal
to the plane (in the sense given by the right-hand circulation rule), and its magnitude
is the product of the total circulating current and the area of the
current loop. More generally, if
 is the atomic current
density at point
is the atomic current
density at point  then the magnetic moment of the atom
is [see Equation (676)]
then the magnetic moment of the atom
is [see Equation (676)]
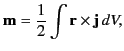 |
(680) |
where the integral is over the volume of the atom. If there are 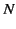 such
atoms or molecules per unit volume then the magnetization,
such
atoms or molecules per unit volume then the magnetization, 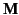 ,
(i.e., the magnetic dipole moment per unit volume) is given
by
,
(i.e., the magnetic dipole moment per unit volume) is given
by
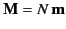 . More generally,
. More generally,
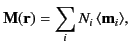 |
(681) |
where
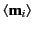 is the average magnetic dipole moment
of the
is the average magnetic dipole moment
of the 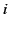 th type of molecule in the vicinity of point
th type of molecule in the vicinity of point  ,
and
,
and 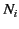 is the average number of such molecules per unit volume at
is the average number of such molecules per unit volume at
 .
.
Consider a general medium that is made up of molecules that are
polarizable, and possess a net magnetic moment.
It is easily demonstrated that any circulation in the magnetization field
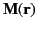 gives rise to an effective current density
gives rise to an effective current density
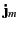 in the medium. In fact,
in the medium. In fact,
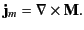 |
(682) |
This current density is called the magnetization current density,
and is usually distinguished from the true current density,
 , which represents the convection of free charges in the
medium. In fact, there is a third type of current called a polarization
current, which is due to the apparent convection of bound charges.
It is easily demonstrated that the polarization current density,
, which represents the convection of free charges in the
medium. In fact, there is a third type of current called a polarization
current, which is due to the apparent convection of bound charges.
It is easily demonstrated that the polarization current density,
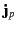 , is given by
, is given by
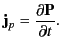 |
(683) |
Thus, the total current density, 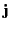 , in the medium is given by
, in the medium is given by
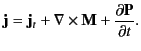 |
(684) |
It must be emphasized that all three terms on the right-hand side of
the previous equation represent
real physical currents, although only the first term is due to the motion
of charges over more than atomic dimensions.
The fourth Maxwell equation, (4), takes the form
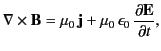 |
(685) |
which can also be written
 |
(686) |
where use has been made of the definition
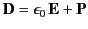 . The previous expression can be rearranged to give
. The previous expression can be rearranged to give
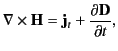 |
(687) |
where
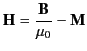 |
(688) |
is termed the magnetic intensity, and has the same dimensions
as 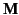 (i.e., magnetic dipole moment per unit volume).
In a steady-state situation, the curl theorem tell us that
(i.e., magnetic dipole moment per unit volume).
In a steady-state situation, the curl theorem tell us that
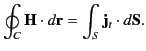 |
(689) |
In other words, the line integral of  around some closed loop
is equal to the flux of true current through any surface attached to that
loop. Unlike the magnetic field
around some closed loop
is equal to the flux of true current through any surface attached to that
loop. Unlike the magnetic field 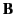 (which specifies
the force
(which specifies
the force
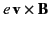 acting on a charge
acting on a charge 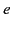 moving
with velocity
moving
with velocity 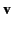 ),
or the magnetization
),
or the magnetization 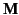 (which specifies the magnetic dipole moment
per unit volume), the magnetic intensity
(which specifies the magnetic dipole moment
per unit volume), the magnetic intensity  has no clear physical
meaning. The only reason for introducing it is that it enables us to
calculate magnetic fields in the presence of magnetic materials without
first having to know the distribution of magnetization currents.
However, this is only possible if we possess a constitutive relation
connecting
has no clear physical
meaning. The only reason for introducing it is that it enables us to
calculate magnetic fields in the presence of magnetic materials without
first having to know the distribution of magnetization currents.
However, this is only possible if we possess a constitutive relation
connecting 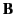 and
and  .
.



Next: Magnetic Susceptibility and Permeability
Up: Magnetostatics in Magnetic Media
Previous: Magnetostatics in Magnetic Media
Richard Fitzpatrick
2014-06-27
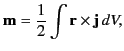
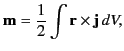
![]() gives rise to an effective current density
gives rise to an effective current density
![]() in the medium. In fact,
in the medium. In fact,