 |
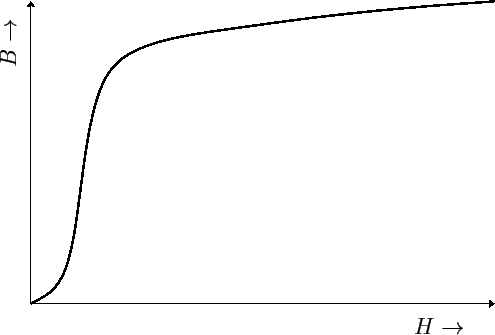
Let us, first, consider an unmagnetized sample of ferromagnetic material.
If the magnetic intensity, which is initially zero, is increased
monotonically, then the ![]() -
-![]() relationship
traces out a curve such as that shown in Figure 2. This is called a
magnetization curve. It is evident that the permeabilities
relationship
traces out a curve such as that shown in Figure 2. This is called a
magnetization curve. It is evident that the permeabilities
![]() derived from the curve (according to the rule
derived from the curve (according to the rule ![]() ) are
always positive, and show a wide range of values. The maximum permeability
occurs at the ``knee'' of the curve. In some materials this
maximum permeability is as large as
) are
always positive, and show a wide range of values. The maximum permeability
occurs at the ``knee'' of the curve. In some materials this
maximum permeability is as large as
![]() . The reason for
the knee in the curve is that the magnetization
. The reason for
the knee in the curve is that the magnetization ![]() reaches
a maximum value in the material, so that
reaches
a maximum value in the material, so that
| (693) |
Next, consider a ferromagnetic sample magnetized by the previously described procedure.
If the magnetic intensity ![]() is decreased then the
is decreased then the ![]() -
-![]() relation does not follow back down the curve of Figure 2, but instead
moves along a new curve, shown in Figure 3, to the point
relation does not follow back down the curve of Figure 2, but instead
moves along a new curve, shown in Figure 3, to the point ![]() .
The magnetization, once established, does not disappear with the removal
of
.
The magnetization, once established, does not disappear with the removal
of ![]() . In fact, it takes a reversed magnetic intensity to
reduce the magnetization to zero. If
. In fact, it takes a reversed magnetic intensity to
reduce the magnetization to zero. If ![]() continues to
build up in the reversed direction then
continues to
build up in the reversed direction then ![]() (and,
hence,
(and,
hence, ![]() ) becomes increasingly negative. Finally,
if
) becomes increasingly negative. Finally,
if ![]() increases again then the operating point follows the lower
curve of Figure 3. Thus, the
increases again then the operating point follows the lower
curve of Figure 3. Thus, the ![]() -
-![]() curve for
increasing
curve for
increasing ![]() is quite different to that for decreasing
is quite different to that for decreasing
![]() . This phenomenon is known as hysteresis.
. This phenomenon is known as hysteresis.
The loop shown in Figure 3 is called the hysteresis loop of the material
in question. The value of ![]() at the point
at the point ![]() is called the
retentivity or remanence. The magnitude of
is called the
retentivity or remanence. The magnitude of ![]() at
the point
at
the point ![]() is called the coercivity. It is
evident that
is called the coercivity. It is
evident that ![]() is negative in the second and fourth quadrants
of the loop, and positive in the first and third quadrants. The shape
of the hysteresis loop depends not only on the nature of
the ferromagnetic material, but also on the maximum value of
is negative in the second and fourth quadrants
of the loop, and positive in the first and third quadrants. The shape
of the hysteresis loop depends not only on the nature of
the ferromagnetic material, but also on the maximum value of ![]() to which the material has been subjected. However, once this maximum
value,
to which the material has been subjected. However, once this maximum
value,
![]() , becomes sufficient to produce saturation in the material, the hysteresis loop does not change shape with any further
increase in
, becomes sufficient to produce saturation in the material, the hysteresis loop does not change shape with any further
increase in
![]() .
.
Ferromagnetic materials are used either to channel magnetic flux
(e.g., around transformer circuits), or as sources of magnetic
field (e.g., permanent magnets). For use as a permanent magnet, the
material is first magnetized by placing it in a strong magnetic
field. However, once the magnet is removed from the external field,
it is subject to a demagnetizing ![]() . Thus, it is vitally important
that a permanent magnet should possess both a large remanence and a large
coercivity. As will become
clear, later on, it is generally a good idea for the ferromagnetic materials
used to channel magnetic flux around transformer circuits to
possess small remanences and small coercivities.
. Thus, it is vitally important
that a permanent magnet should possess both a large remanence and a large
coercivity. As will become
clear, later on, it is generally a good idea for the ferromagnetic materials
used to channel magnetic flux around transformer circuits to
possess small remanences and small coercivities.