Cassini's laws
Consider Figure 8.13. Here,  ,
, 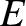 , and
, and  , represent the center of the Moon, the center of the Earth,
and the north ecliptic pole, respectively.
Moreover,
, represent the center of the Moon, the center of the Earth,
and the north ecliptic pole, respectively.
Moreover,  is the instantaneous normal to the Moon's equatorial plane, and
is the instantaneous normal to the Moon's equatorial plane, and 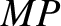 the
instantaneous normal to the Moon's orbital plane. Let
the
instantaneous normal to the Moon's orbital plane. Let  ,
,
 ,
,
 , and
, and  be
unit vectors parallel to
be
unit vectors parallel to 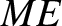 ,
,  ,
, 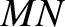 , and
, and 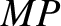 , respectively. The fixed angle,
, respectively. The fixed angle,
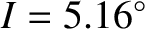 , subtended between the
directions of
, subtended between the
directions of  and
and
 , represents the fixed inclination of the Moon's orbital plane to the ecliptic
plane. Furthermore, as is well known, because of
the perturbing action of the Sun, the normal to the Moon's orbital plane,
, represents the fixed inclination of the Moon's orbital plane to the ecliptic
plane. Furthermore, as is well known, because of
the perturbing action of the Sun, the normal to the Moon's orbital plane,  , precesses about
the normal to the ecliptic plane,
, precesses about
the normal to the ecliptic plane,
 , in the opposite sense to the Moon's orbital motion, such that it completes a full circuit every
, in the opposite sense to the Moon's orbital motion, such that it completes a full circuit every  years. (See Chapter 11.) Recall that precession in the opposite sense to
orbital motion is usually termed regression.
years. (See Chapter 11.) Recall that precession in the opposite sense to
orbital motion is usually termed regression.
In 1693, the astronomer Gian Domenico Cassini (1625–1712) formulated a set of empirical laws that succinctly describe
the Moon's axial rotation. According to these laws:
- The Moon spins at a uniform rate that matches its mean orbital rotation rate.
- The normal to the Moon's equatorial plane subtends a fixed angle,
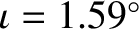 , with the normal to the ecliptic plane.
, with the normal to the ecliptic plane.
- The normal to the Moon's equatorial plane, the normal to the Moon's
orbital plane, and the normal to the ecliptic plane, are coplanar vectors that are orientated such that the latter vector
lies between the other two.
Law 1 effectively states that the Moon is locked in a 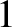 :
: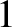 spin-orbit resonance. (See Section 8.11.) Let the
spin-orbit resonance. (See Section 8.11.) Let the  -,
-,  -, and
-, and
 -axes be the Moon's principal axes of rotation, and let
-axes be the Moon's principal axes of rotation, and let
 ,
,
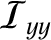 , and
, and
 be the corresponding principal moments of inertia. Furthermore, let us label the principal axes such that the Moon's equatorial
plane corresponds to the
be the corresponding principal moments of inertia. Furthermore, let us label the principal axes such that the Moon's equatorial
plane corresponds to the  -
- plane, the normal to the equatorial plane corresponds to the
plane, the normal to the equatorial plane corresponds to the  -axis, and
-axis, and
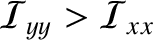 .
In this case, as we saw in the previous section, a
.
In this case, as we saw in the previous section, a 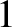 :
: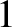 spin-orbit resonant state is such that the Moon's
spin-orbit resonant state is such that the Moon's
 -axis always points approximately in the direction of the Earth; that is,
-axis always points approximately in the direction of the Earth; that is,  is almost parallel to the
is almost parallel to the  -axis.
-axis.
Law 2 states that the angle, 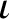 , subtended between
, subtended between
 and
and
 is fixed. Moreover, because the angles
is fixed. Moreover, because the angles  and
and 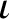 are both small (when expressed in radians), we deduce that the vectors
are both small (when expressed in radians), we deduce that the vectors
 and
and  are almost parallel to
are almost parallel to
 .
.
Law 3 states that the vectors
 ,
,
 , and
, and
 all lie in the same plane, with
all lie in the same plane, with
 and
and  on opposite sides of
on opposite sides of
 . In other words, as the normal to the Moon's orbital plane,
. In other words, as the normal to the Moon's orbital plane,  , regresses about the
normal to the ecliptic plane,
, regresses about the
normal to the ecliptic plane,
 , the normal to the Moon's equatorial plane,
, the normal to the Moon's equatorial plane,
 , regresses at the same
rate, such that
, regresses at the same
rate, such that
 is always directly opposite
is always directly opposite  with respect to
with respect to
 .
.
Figure 8.13:
Geometry of Cassini's laws.
|
|
Cassini's first law was accounted for in the previous section. The ultimate aim of this section is to account for Cassini's second and
third laws. Our approach is largely based on that of Danby (1992). In order to simplify the analysis, we shall assume that the Moon orbits around the Earth, at the
uniform angular velocity,  , in a circular orbit of major radius
, in a circular orbit of major radius  . When expressed in terms of the
. When expressed in terms of the
 ,
,  ,
,  coordinate system,
coordinate system,

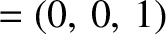 . Furthermore, because the unit vectors
. Furthermore, because the unit vectors
 and
and  are
almost parallel to
are
almost parallel to
 , we can write
, we can write
where 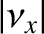 ,
, 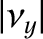 ,
,  ,
,
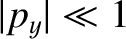 . Similarly, because the unit vector
. Similarly, because the unit vector  is almost
parallel to the
is almost
parallel to the  -axis, we have
-axis, we have
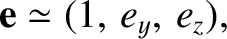 |
(8.192) |
where 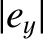 ,
,
 . The position vector,
. The position vector,
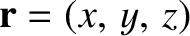 , of the center of the Earth with respect to the
center of the Moon is written
, of the center of the Earth with respect to the
center of the Moon is written
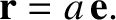 |
(8.193) |
Finally, given Cassini's first law, and assuming that the Moon's spin axis is almost parallel to the  -axis, the
Moon's spin angular velocity takes the form
-axis, the
Moon's spin angular velocity takes the form
 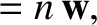 |
(8.194) |
Here, 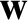 is a unit vector such that
is a unit vector such that
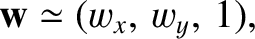 |
(8.195) |
where 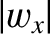 ,
,
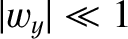 .
.
According to Equations (8.150), (8.151),
(8.153), and (8.154),
because  and
and
 . Here,
Note that
. Here,
Note that  ,
,
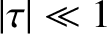 because the Moon is almost spherically symmetric. To second order in small
quantities, Equations (8.196) and (8.197) yield
where use has been made of Equations (8.192)–(8.195).
because the Moon is almost spherically symmetric. To second order in small
quantities, Equations (8.196) and (8.197) yield
where use has been made of Equations (8.192)–(8.195).
The unit
vector
 is stationary in an inertial frame whose coordinate axes are fixed with respect to distant stars.
Hence, in the
is stationary in an inertial frame whose coordinate axes are fixed with respect to distant stars.
Hence, in the  ,
,  ,
,  body frame, which rotates with respect to the
aforementioned fixed frame at the angular velocity
body frame, which rotates with respect to the
aforementioned fixed frame at the angular velocity
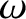 ,
we have (see Section 6.2)
,
we have (see Section 6.2)
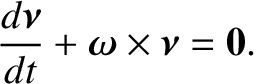 |
(8.202) |
It follows, from Equations (8.190), (8.194), and (8.195), that
These expressions can be combined with Equations (8.200) and (8.201) to give
It now remains to express 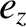 in terms of
in terms of 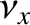 and
and 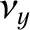 .
.
By definition,  is normal to
is normal to  , as the vector
, as the vector  lies in the plane of the Moon's orbit.
Hence, according to Equations (8.191) and (8.192),
lies in the plane of the Moon's orbit.
Hence, according to Equations (8.191) and (8.192),
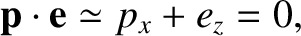 |
(8.207) |
which implies that
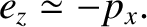 |
(8.208) |
Let 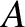 be the ascending node of the Earth's apparent orbit about the Moon (which implies that
be the ascending node of the Earth's apparent orbit about the Moon (which implies that 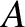 is the
descending node of the Moon's actual orbit about the Earth), and
let
is the
descending node of the Moon's actual orbit about the Earth), and
let 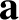 be a unit vector parallel to
be a unit vector parallel to  . See Figure 8.13 and Section 4.12. By definition,
. See Figure 8.13 and Section 4.12. By definition,
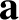 is normal to both
is normal to both  and
and
 . In fact, we can write
. In fact, we can write
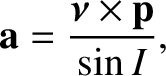 |
(8.209) |
where  is the angle subtended between the vectors
is the angle subtended between the vectors  and
and
 . It follows from Equations (8.190), (8.191),
and the fact that
. It follows from Equations (8.190), (8.191),
and the fact that  is small, that
is small, that
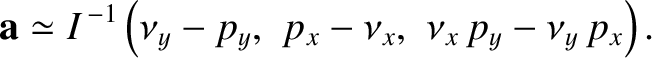 |
(8.210) |
Now,
where 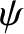 is the angle subtended between
is the angle subtended between 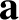 and
and  . See Figure 8.13.
Thus, Equations (8.191), (8.192), and (8.210) yield
and
. See Figure 8.13.
Thus, Equations (8.191), (8.192), and (8.210) yield
and
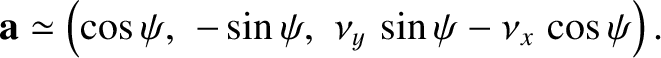 |
(8.215) |
In fact, 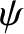 is the longitude of the Earth relative to the ascending node of its apparent orbit around the Moon. It follows that
is the longitude of the Earth relative to the ascending node of its apparent orbit around the Moon. It follows that
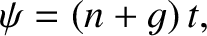 |
(8.216) |
where 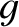 is the uniform regression rate of the Earth's apparent ascending node (which is the
same as the regression rate of the true ascending node of the Moon's orbit around the Earth). Here,
for the sake of simplicity, we have assumed that the Earth
passes through its apparent ascending node at time
is the uniform regression rate of the Earth's apparent ascending node (which is the
same as the regression rate of the true ascending node of the Moon's orbit around the Earth). Here,
for the sake of simplicity, we have assumed that the Earth
passes through its apparent ascending node at time 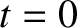 .
Hence, Equations (8.205), (8.206), (8.208), (8.213), and
(8.216) can be combined to give
.
Hence, Equations (8.205), (8.206), (8.208), (8.213), and
(8.216) can be combined to give
The previous two equations govern the Moon's physical libration in latitude. As is the
case for libration in longitude, there are both free and
forced modes. The free modes satisfy
Let us search for solutions of the form
where
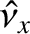 ,
,
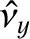 ,
, 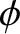 are constants.
It follows that
are constants.
It follows that
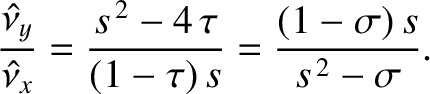 |
(8.223) |
Given that  and
and  are both small compared to unity, two independent free libration modes can be
derived from the preceding expression. The first mode is such that
are both small compared to unity, two independent free libration modes can be
derived from the preceding expression. The first mode is such that
 and
and
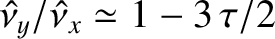 , whereas the second is such that
, whereas the second is such that
 and
and
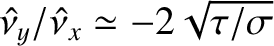 .
In the Moon's body frame, these modes cause the normal to the ecliptic plane,
.
In the Moon's body frame, these modes cause the normal to the ecliptic plane,

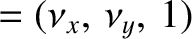 , to
precess about the normal to the Moon's equatorial plane,
, to
precess about the normal to the Moon's equatorial plane,

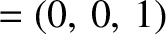 , in such a manner that
where
, in such a manner that
where
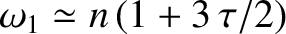 ,
,
 ,
,
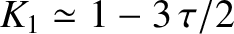 ,
,
 , and the constants
, and the constants 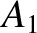 ,
, 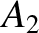 ,
, 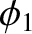 ,
, 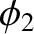 are arbitrary.
The observed values of
are arbitrary.
The observed values of  ,
, 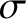 , and
, and 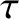 are
are
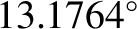 per day,
per day,
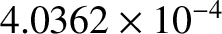 ,
and
,
and
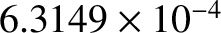 , respectively (Konopliv et al. 1998; Dickey et al. 1994). [Actually,
, respectively (Konopliv et al. 1998; Dickey et al. 1994). [Actually, 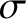 and
and 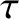 are measured by fitting
observations of lunar libration obtained from laser ranging to the theory described here.] Thus, it follows that
are measured by fitting
observations of lunar libration obtained from laser ranging to the theory described here.] Thus, it follows that
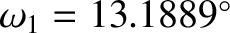 per day,
per day,
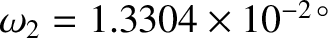 per day,
per day,
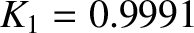 , and
, and
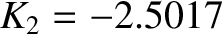 . In the body frame, the first mode causes
. In the body frame, the first mode causes
 to regress about
to regress about
 with a period of
with a period of 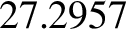 days, whereas the second mode causes
days, whereas the second mode causes
 to precess
about
to precess
about
 with a period of
with a period of 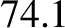 years. Both these modes of libration have been detected by means of
lunar laser ranging. The measured amplitude of the first mode is
years. Both these modes of libration have been detected by means of
lunar laser ranging. The measured amplitude of the first mode is
 , whereas that of the second mode is
, whereas that of the second mode is
 (Jin and Li 1996). Incidentally, the second mode is very
similar in nature to the Chandler wobble of the Earth. (See Section 8.8.)
Note that if
(Jin and Li 1996). Incidentally, the second mode is very
similar in nature to the Chandler wobble of the Earth. (See Section 8.8.)
Note that if 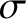 and
and 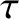 were of opposite sign—that is, if
were of opposite sign—that is, if
 were intermediate between
were intermediate between
 and
and
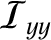 —the second mode of libration would grow exponentially in time, rather than oscillate at a constant amplitude; in other words, the Moon's
spin state would be unstable. In fact, the Moon's principal axes
of rotation are orientated such that
—the second mode of libration would grow exponentially in time, rather than oscillate at a constant amplitude; in other words, the Moon's
spin state would be unstable. In fact, the Moon's principal axes
of rotation are orientated such that
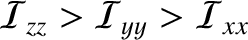 , which ensures that the Moon spins in a stable manner.
, which ensures that the Moon spins in a stable manner.
Let us now search for forced solutions of Equations (8.217) and (8.218) of the form
where
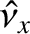 ,
,
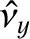 are constants. It follows
that
Hence, recalling that
are constants. It follows
that
Hence, recalling that 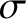 ,
, 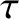 , and
, and 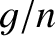 are all small compared to unity, we obtain the
following mode of forced libration:
In the Moon's body frame, this mode causes the vectors
are all small compared to unity, we obtain the
following mode of forced libration:
In the Moon's body frame, this mode causes the vectors
 and
and  to regress about
to regress about
 (i.e., the
(i.e., the  -axis) in such a manner that
where
-axis) in such a manner that
where
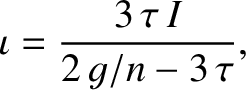 |
(8.234) |
and use has been made of Equations (8.213), (8.214), and (8.216).
Because the observed values of  ,
, 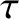 , and
, and 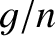 are
are
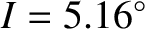 ,
,
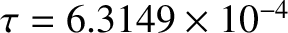 , and
, and
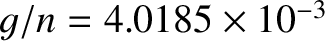 (Konopliv et al. 1998; Dickey et al. 1994; Yoder 1995), we deduce that
(Konopliv et al. 1998; Dickey et al. 1994; Yoder 1995), we deduce that
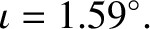 |
(8.235) |
According to Equation (8.232),
 regresses around
regresses around
 , with a
period of
, with a
period of 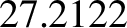 days (i.e., a draconic month), in such a manner that
days (i.e., a draconic month), in such a manner that
 subtends
a fixed angle of
subtends
a fixed angle of
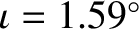 with respect to
with respect to
 . This accounts for Cassini's second law.
According to Equation (8.233),
. This accounts for Cassini's second law.
According to Equation (8.233),  simultaneously regress around
simultaneously regress around
 , with the same period, in such a manner that
, with the same period, in such a manner that



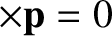 . In other words,
the three vectors
. In other words,
the three vectors
 ,
,
 , and
, and  always lie in the same plane. Moreover, it is
clear that
always lie in the same plane. Moreover, it is
clear that
 is intermediate between
is intermediate between
 and
and  . This accounts for Cassini's third law.
The angle
. This accounts for Cassini's third law.
The angle
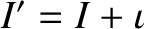 , subtended between
, subtended between
 and
and  , which
is also the angle of inclination between the Moon's equatorial and orbital planes, takes the
fixed value
, which
is also the angle of inclination between the Moon's equatorial and orbital planes, takes the
fixed value
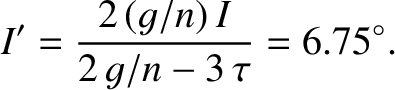 |
(8.236) |
Note that this angle would be zero in the absence of any regression of the Moon's orbital ascending node (i.e., if
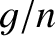 were zero). In other words,
the nonzero angle of inclination between the Moon's equatorial and orbital planes is a direct consequence of this regression, which is
ultimately due to the perturbing action of the Sun. Because the regression of the Moon's orbital ascending node
is also responsible for the forced nutation of the Earth's axis of rotation (see Section 8.10), it follows that this nutation is closely related to the forced inclination between the Moon's equatorial and orbital planes.
were zero). In other words,
the nonzero angle of inclination between the Moon's equatorial and orbital planes is a direct consequence of this regression, which is
ultimately due to the perturbing action of the Sun. Because the regression of the Moon's orbital ascending node
is also responsible for the forced nutation of the Earth's axis of rotation (see Section 8.10), it follows that this nutation is closely related to the forced inclination between the Moon's equatorial and orbital planes.
 ,
,  , and
, and  , represent the center of the Moon, the center of the Earth,
and the north ecliptic pole, respectively.
Moreover,
, represent the center of the Moon, the center of the Earth,
and the north ecliptic pole, respectively.
Moreover,  is the instantaneous normal to the Moon's equatorial plane, and
is the instantaneous normal to the Moon's equatorial plane, and  the
instantaneous normal to the Moon's orbital plane. Let
the
instantaneous normal to the Moon's orbital plane. Let  ,
,
 ,
,
 , and
, and  be
unit vectors parallel to
be
unit vectors parallel to 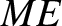 ,
,  ,
, 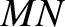 , and
, and 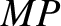 , respectively. The fixed angle,
, respectively. The fixed angle,
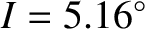 , subtended between the
directions of
, subtended between the
directions of  and
and
 , represents the fixed inclination of the Moon's orbital plane to the ecliptic
plane. Furthermore, as is well known, because of
the perturbing action of the Sun, the normal to the Moon's orbital plane,
, represents the fixed inclination of the Moon's orbital plane to the ecliptic
plane. Furthermore, as is well known, because of
the perturbing action of the Sun, the normal to the Moon's orbital plane,  , precesses about
the normal to the ecliptic plane,
, precesses about
the normal to the ecliptic plane,
 , in the opposite sense to the Moon's orbital motion, such that it completes a full circuit every
, in the opposite sense to the Moon's orbital motion, such that it completes a full circuit every  years. (See Chapter 11.) Recall that precession in the opposite sense to
orbital motion is usually termed regression.
years. (See Chapter 11.) Recall that precession in the opposite sense to
orbital motion is usually termed regression.
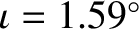 , with the normal to the ecliptic plane.
, with the normal to the ecliptic plane.
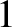 :
: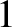 spin-orbit resonance. (See Section 8.11.) Let the
spin-orbit resonance. (See Section 8.11.) Let the  -,
-,  -, and
-, and
 -axes be the Moon's principal axes of rotation, and let
-axes be the Moon's principal axes of rotation, and let
 ,
,
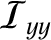 , and
, and
 be the corresponding principal moments of inertia. Furthermore, let us label the principal axes such that the Moon's equatorial
plane corresponds to the
be the corresponding principal moments of inertia. Furthermore, let us label the principal axes such that the Moon's equatorial
plane corresponds to the  -
- plane, the normal to the equatorial plane corresponds to the
plane, the normal to the equatorial plane corresponds to the  -axis, and
-axis, and
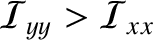 .
In this case, as we saw in the previous section, a
.
In this case, as we saw in the previous section, a  :
: spin-orbit resonant state is such that the Moon's
spin-orbit resonant state is such that the Moon's
 -axis always points approximately in the direction of the Earth; that is,
-axis always points approximately in the direction of the Earth; that is,  is almost parallel to the
is almost parallel to the  -axis.
-axis.
 , subtended between
, subtended between
 and
and
 is fixed. Moreover, because the angles
is fixed. Moreover, because the angles  and
and 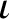 are both small (when expressed in radians), we deduce that the vectors
are both small (when expressed in radians), we deduce that the vectors
 and
and  are almost parallel to
are almost parallel to
 .
.
 ,
,
 , and
, and
 all lie in the same plane, with
all lie in the same plane, with
 and
and  on opposite sides of
on opposite sides of
 . In other words, as the normal to the Moon's orbital plane,
. In other words, as the normal to the Moon's orbital plane,  , regresses about the
normal to the ecliptic plane,
, regresses about the
normal to the ecliptic plane,
 , the normal to the Moon's equatorial plane,
, the normal to the Moon's equatorial plane,
 , regresses at the same
rate, such that
, regresses at the same
rate, such that
 is always directly opposite
is always directly opposite  with respect to
with respect to
 .
.
 , in a circular orbit of major radius
, in a circular orbit of major radius  . When expressed in terms of the
. When expressed in terms of the
 ,
,  ,
,  coordinate system,
coordinate system,

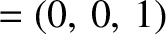 . Furthermore, because the unit vectors
. Furthermore, because the unit vectors
 and
and  are
almost parallel to
are
almost parallel to
 , we can write
, we can write
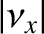 ,
, 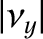 ,
,  ,
,
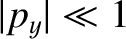 . Similarly, because the unit vector
. Similarly, because the unit vector  is almost
parallel to the
is almost
parallel to the  -axis, we have
where
-axis, we have
where 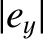 ,
,
 . The position vector,
. The position vector,
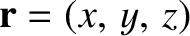 , of the center of the Earth with respect to the
center of the Moon is written
Finally, given Cassini's first law, and assuming that the Moon's spin axis is almost parallel to the
, of the center of the Earth with respect to the
center of the Moon is written
Finally, given Cassini's first law, and assuming that the Moon's spin axis is almost parallel to the  -axis, the
Moon's spin angular velocity takes the form
Here,
-axis, the
Moon's spin angular velocity takes the form
Here, 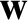 is a unit vector such that
where
is a unit vector such that
where 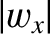 ,
,
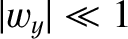 .
.
 and
and
 . Here,
Note that
. Here,
Note that  ,
,
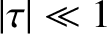 because the Moon is almost spherically symmetric. To second order in small
quantities, Equations (8.196) and (8.197) yield
where use has been made of Equations (8.192)–(8.195).
because the Moon is almost spherically symmetric. To second order in small
quantities, Equations (8.196) and (8.197) yield
where use has been made of Equations (8.192)–(8.195).
 is stationary in an inertial frame whose coordinate axes are fixed with respect to distant stars.
Hence, in the
is stationary in an inertial frame whose coordinate axes are fixed with respect to distant stars.
Hence, in the  ,
,  ,
,  body frame, which rotates with respect to the
aforementioned fixed frame at the angular velocity
body frame, which rotates with respect to the
aforementioned fixed frame at the angular velocity
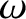 ,
we have (see Section 6.2)
,
we have (see Section 6.2)
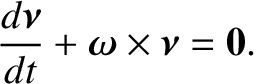

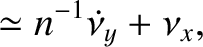
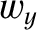
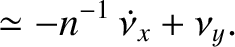
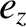 in terms of
in terms of 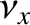 and
and 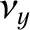 .
.
 is normal to
is normal to  , as the vector
, as the vector  lies in the plane of the Moon's orbit.
Hence, according to Equations (8.191) and (8.192),
lies in the plane of the Moon's orbit.
Hence, according to Equations (8.191) and (8.192),
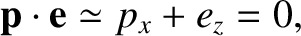
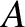 be the ascending node of the Earth's apparent orbit about the Moon (which implies that
be the ascending node of the Earth's apparent orbit about the Moon (which implies that 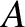 is the
descending node of the Moon's actual orbit about the Earth), and
let
is the
descending node of the Moon's actual orbit about the Earth), and
let 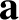 be a unit vector parallel to
be a unit vector parallel to  . See Figure 8.13 and Section 4.12. By definition,
. See Figure 8.13 and Section 4.12. By definition,
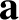 is normal to both
is normal to both  and
and
 . In fact, we can write
. In fact, we can write
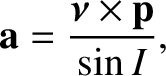
 is the angle subtended between the vectors
is the angle subtended between the vectors  and
and
 . It follows from Equations (8.190), (8.191),
and the fact that
. It follows from Equations (8.190), (8.191),
and the fact that  is small, that
Now,
is small, that
Now,
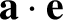
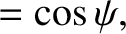
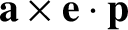
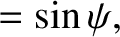
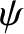 is the angle subtended between
is the angle subtended between 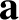 and
and  . See Figure 8.13.
Thus, Equations (8.191), (8.192), and (8.210) yield
and
. See Figure 8.13.
Thus, Equations (8.191), (8.192), and (8.210) yield
and
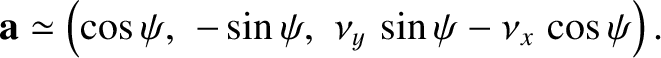
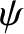 is the longitude of the Earth relative to the ascending node of its apparent orbit around the Moon. It follows that
where
is the longitude of the Earth relative to the ascending node of its apparent orbit around the Moon. It follows that
where 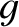 is the uniform regression rate of the Earth's apparent ascending node (which is the
same as the regression rate of the true ascending node of the Moon's orbit around the Earth). Here,
for the sake of simplicity, we have assumed that the Earth
passes through its apparent ascending node at time
is the uniform regression rate of the Earth's apparent ascending node (which is the
same as the regression rate of the true ascending node of the Moon's orbit around the Earth). Here,
for the sake of simplicity, we have assumed that the Earth
passes through its apparent ascending node at time 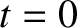 .
Hence, Equations (8.205), (8.206), (8.208), (8.213), and
(8.216) can be combined to give
.
Hence, Equations (8.205), (8.206), (8.208), (8.213), and
(8.216) can be combined to give
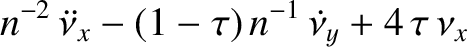

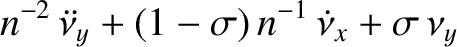

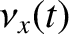
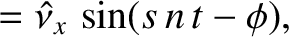
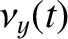
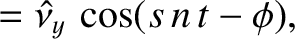
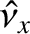 ,
,
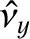 ,
, 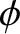 are constants.
It follows that
are constants.
It follows that
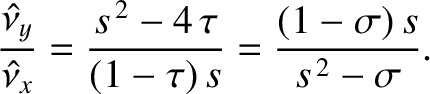
 and
and  are both small compared to unity, two independent free libration modes can be
derived from the preceding expression. The first mode is such that
are both small compared to unity, two independent free libration modes can be
derived from the preceding expression. The first mode is such that
 and
and
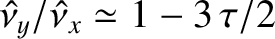 , whereas the second is such that
, whereas the second is such that
 and
and
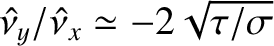 .
In the Moon's body frame, these modes cause the normal to the ecliptic plane,
.
In the Moon's body frame, these modes cause the normal to the ecliptic plane,

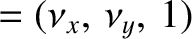 , to
precess about the normal to the Moon's equatorial plane,
, to
precess about the normal to the Moon's equatorial plane,

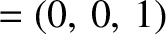 , in such a manner that
, in such a manner that
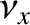
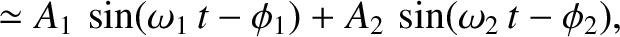
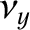
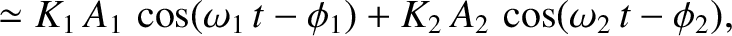
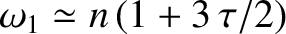 ,
,
 ,
,
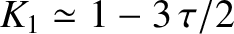 ,
,
 , and the constants
, and the constants 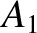 ,
, 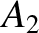 ,
, 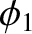 ,
, 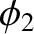 are arbitrary.
The observed values of
are arbitrary.
The observed values of  ,
, 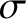 , and
, and 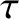 are
are
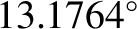 per day,
per day,
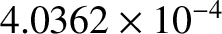 ,
and
,
and
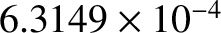 , respectively (Konopliv et al. 1998; Dickey et al. 1994). [Actually,
, respectively (Konopliv et al. 1998; Dickey et al. 1994). [Actually, 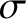 and
and 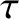 are measured by fitting
observations of lunar libration obtained from laser ranging to the theory described here.] Thus, it follows that
are measured by fitting
observations of lunar libration obtained from laser ranging to the theory described here.] Thus, it follows that
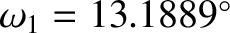 per day,
per day,
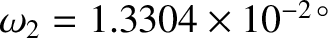 per day,
per day,
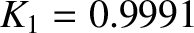 , and
, and
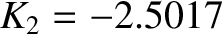 . In the body frame, the first mode causes
. In the body frame, the first mode causes
 to regress about
to regress about
 with a period of
with a period of 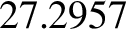 days, whereas the second mode causes
days, whereas the second mode causes
 to precess
about
to precess
about
 with a period of
with a period of 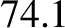 years. Both these modes of libration have been detected by means of
lunar laser ranging. The measured amplitude of the first mode is
years. Both these modes of libration have been detected by means of
lunar laser ranging. The measured amplitude of the first mode is
 , whereas that of the second mode is
, whereas that of the second mode is
 (Jin and Li 1996). Incidentally, the second mode is very
similar in nature to the Chandler wobble of the Earth. (See Section 8.8.)
Note that if
(Jin and Li 1996). Incidentally, the second mode is very
similar in nature to the Chandler wobble of the Earth. (See Section 8.8.)
Note that if 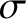 and
and 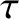 were of opposite sign—that is, if
were of opposite sign—that is, if
 were intermediate between
were intermediate between
 and
and
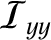 —the second mode of libration would grow exponentially in time, rather than oscillate at a constant amplitude; in other words, the Moon's
spin state would be unstable. In fact, the Moon's principal axes
of rotation are orientated such that
—the second mode of libration would grow exponentially in time, rather than oscillate at a constant amplitude; in other words, the Moon's
spin state would be unstable. In fact, the Moon's principal axes
of rotation are orientated such that
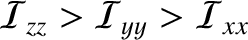 , which ensures that the Moon spins in a stable manner.
, which ensures that the Moon spins in a stable manner.
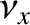
![$\displaystyle =\skew{3}\hat{\nu}_x\,\sin[(n+g)\,t],$](img2056.png)
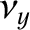
![$\displaystyle =\skew{3}\hat{\nu}_y\,\cos[(n+g)\,t],$](img2057.png)
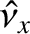 ,
,
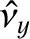 are constants. It follows
that
are constants. It follows
that
![$\displaystyle \left[4\,\tau-(1+g/n)^{\,2}\right]\skew{3}\hat{\nu}_x + (1-\tau)\,(1+g/n)\,\skew{3}\hat{\nu}_y$](img2058.png)
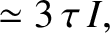
![$\displaystyle (1-\sigma)\,(1+g/n)\,\skew{3}\hat{\nu}_x+\left[\sigma-(1+g/n)^{\,2}\right]\skew{3}\hat{\nu}_y$](img2060.png)

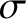 ,
, 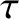 , and
, and 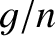 are all small compared to unity, we obtain the
following mode of forced libration:
are all small compared to unity, we obtain the
following mode of forced libration:
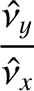
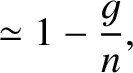

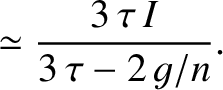
 and
and  to regress about
to regress about
 (i.e., the
(i.e., the  -axis) in such a manner that
where
-axis) in such a manner that
where
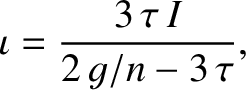
 ,
, 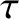 , and
, and 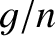 are
are
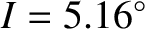 ,
,
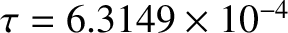 , and
, and
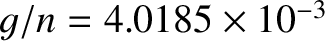 (Konopliv et al. 1998; Dickey et al. 1994; Yoder 1995), we deduce that
(Konopliv et al. 1998; Dickey et al. 1994; Yoder 1995), we deduce that
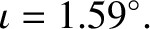
 regresses around
regresses around
 , with a
period of
, with a
period of 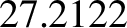 days (i.e., a draconic month), in such a manner that
days (i.e., a draconic month), in such a manner that
 subtends
a fixed angle of
subtends
a fixed angle of
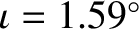 with respect to
with respect to
 . This accounts for Cassini's second law.
According to Equation (8.233),
. This accounts for Cassini's second law.
According to Equation (8.233),  simultaneously regress around
simultaneously regress around
 , with the same period, in such a manner that
, with the same period, in such a manner that



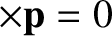 . In other words,
the three vectors
. In other words,
the three vectors
 ,
,
 , and
, and  always lie in the same plane. Moreover, it is
clear that
always lie in the same plane. Moreover, it is
clear that
 is intermediate between
is intermediate between
 and
and  . This accounts for Cassini's third law.
The angle
. This accounts for Cassini's third law.
The angle
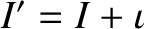 , subtended between
, subtended between
 and
and  , which
is also the angle of inclination between the Moon's equatorial and orbital planes, takes the
fixed value
, which
is also the angle of inclination between the Moon's equatorial and orbital planes, takes the
fixed value
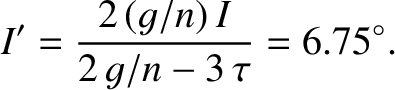
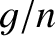 were zero). In other words,
the nonzero angle of inclination between the Moon's equatorial and orbital planes is a direct consequence of this regression, which is
ultimately due to the perturbing action of the Sun. Because the regression of the Moon's orbital ascending node
is also responsible for the forced nutation of the Earth's axis of rotation (see Section 8.10), it follows that this nutation is closely related to the forced inclination between the Moon's equatorial and orbital planes.
were zero). In other words,
the nonzero angle of inclination between the Moon's equatorial and orbital planes is a direct consequence of this regression, which is
ultimately due to the perturbing action of the Sun. Because the regression of the Moon's orbital ascending node
is also responsible for the forced nutation of the Earth's axis of rotation (see Section 8.10), it follows that this nutation is closely related to the forced inclination between the Moon's equatorial and orbital planes.