Next: Planetary orbits Up: Keplerian orbits Previous: Elliptic orbits
Let us characterize all planetary orbits using a common Cartesian coordinate
system 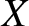 ,
, 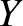 ,
, 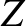 , centered on the Sun. See Figure 4.6. The
, centered on the Sun. See Figure 4.6. The 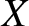 -
-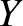 plane defines a reference plane,
which is chosen to be the ecliptic plane (i.e., the plane of the Earth's orbit), with the
plane defines a reference plane,
which is chosen to be the ecliptic plane (i.e., the plane of the Earth's orbit), with the
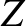 -axis pointing towards the ecliptic north pole (i.e., the direction normal to the ecliptic plane in a northward sense).
Likewise, the
-axis pointing towards the ecliptic north pole (i.e., the direction normal to the ecliptic plane in a northward sense).
Likewise, the
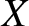 -axis defines a reference direction, which is chosen
to point in the direction of the vernal equinox (i.e., the point in the Earth's sky at which the apparent orbit of the
Sun passes through the extension of the Earth's equatorial plane from south to north). Suppose that the plane of a given
planetary orbit is inclined at an angle
-axis defines a reference direction, which is chosen
to point in the direction of the vernal equinox (i.e., the point in the Earth's sky at which the apparent orbit of the
Sun passes through the extension of the Earth's equatorial plane from south to north). Suppose that the plane of a given
planetary orbit is inclined at an angle  to the reference plane. The point
at which this orbit crosses the reference plane in the direction of
increasing
to the reference plane. The point
at which this orbit crosses the reference plane in the direction of
increasing 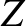 is termed its ascending node. The angle
is termed its ascending node. The angle
 subtended between the reference direction and the direction of the ascending node
is termed the longitude of the
ascending node. Finally, the angle,
subtended between the reference direction and the direction of the ascending node
is termed the longitude of the
ascending node. Finally, the angle, 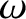 , subtended between the
direction of the ascending node and the direction of the orbit's perihelion is termed
the argument of the perihelion.
, subtended between the
direction of the ascending node and the direction of the orbit's perihelion is termed
the argument of the perihelion.
Let us define a second Cartesian coordinate system  ,
,  ,
,  , also
centered on the Sun. Let the
, also
centered on the Sun. Let the  -
- plane coincide with the plane of a particular planetary orbit,
and let the
plane coincide with the plane of a particular planetary orbit,
and let the  -axis point towards the orbit's perihelion point. Clearly,
we can transform from the
-axis point towards the orbit's perihelion point. Clearly,
we can transform from the  ,
,  ,
,  system to the
system to the 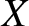 ,
, 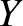 ,
, 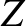 system via a series of three rotations of the coordinate system: first,
a rotation through an angle
system via a series of three rotations of the coordinate system: first,
a rotation through an angle 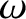 about the
about the  -axis (looking down the
axis); second, a rotation through an angle
-axis (looking down the
axis); second, a rotation through an angle  about the new
about the new  -axis; and
finally, a rotation through an angle
-axis; and
finally, a rotation through an angle
 about the new
about the new  -axis.
It thus follows from standard coordinate transformation theory (see Section A.6) that
-axis.
It thus follows from standard coordinate transformation theory (see Section A.6) that
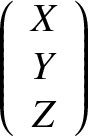 |
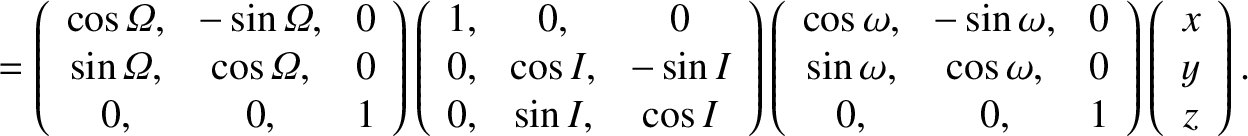 |
|
| (4.71) |
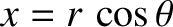 ,
,
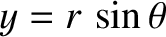 , and
, and  . Hence,
Thus, a general planetary orbit is determined by Equations (4.67)–(4.70) and (4.72)–(4.74), and is therefore parameterized
by six orbital elements: the major radius,
. Hence,
Thus, a general planetary orbit is determined by Equations (4.67)–(4.70) and (4.72)–(4.74), and is therefore parameterized
by six orbital elements: the major radius,  ; the time of perihelion passage,
; the time of perihelion passage, 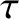 ; the eccentricity,
; the eccentricity,  ;
the inclination (to the ecliptic plane),
;
the inclination (to the ecliptic plane),  ; the argument of the perihelion,
; the argument of the perihelion,
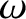 ; and the longitude of the ascending node,
; and the longitude of the ascending node,
 . [The mean orbital angular velocity, in radians per year, is
. [The mean orbital angular velocity, in radians per year, is
 , where
, where  is measured in astronomical units. Here, an astronomical unit is the mean Earth-Sun distance, and
corresponds to
is measured in astronomical units. Here, an astronomical unit is the mean Earth-Sun distance, and
corresponds to
 (Yoder 1995).]
(Yoder 1995).]
In low-inclination orbits, the argument of the perihelion is usually replaced by
which is termed the longitude of the perihelion. Likewise, the time of perihelion passage,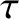 , is often replaced by the mean
longitude at
, is often replaced by the mean
longitude at 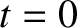 —otherwise known as the mean longitude at epoch—where the mean longitude is defined
—otherwise known as the mean longitude at epoch—where the mean longitude is defined
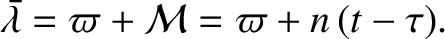 |
(4.76) |
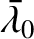 denotes the mean longitude at epoch (
denotes the mean longitude at epoch (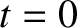 ) then
where
) then
where
 . Another common alternative to
. Another common alternative to 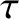 is the mean anomaly at epoch,
is the mean anomaly at epoch,
 |
(4.78) |
1pt
|
The heliocentric (i.e., as seen from the Sun) position of a planet is most conveniently expressed in terms of
its
ecliptic longitude,  , and ecliptic latitude,
, and ecliptic latitude, 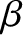 . This type of longitude and latitude is referred to the
ecliptic plane, with the Sun as the origin. Moreover, the vernal equinox is defined to be the zero of longitude. It follows that
. This type of longitude and latitude is referred to the
ecliptic plane, with the Sun as the origin. Moreover, the vernal equinox is defined to be the zero of longitude. It follows that
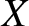 ,
, 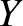 ,
, 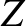 ) are the heliocentric Cartesian coordinates of the planet.
) are the heliocentric Cartesian coordinates of the planet.