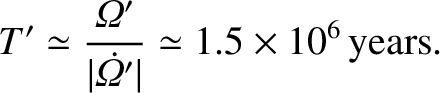Tidal torques
The fact that there is a time lag between the Moon passing overhead and the corresponding maximum net tidal elongation of the Earth and the oceans suggests the
physical scenario illustrated in Figure 6.10. According to this scenario, the Moon, which is of mass  and which is
treated as a point particle, orbits the Earth (it actually orbits the center of mass of the Earth-Moon system, but this
amounts to almost the same thing) in an approximately circular orbit of radius
and which is
treated as a point particle, orbits the Earth (it actually orbits the center of mass of the Earth-Moon system, but this
amounts to almost the same thing) in an approximately circular orbit of radius  . Moreover, the orbital angular velocity of the
Moon is [see Equation (6.59)]
. Moreover, the orbital angular velocity of the
Moon is [see Equation (6.59)]
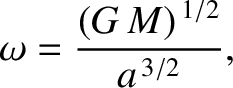 |
(6.87) |
where
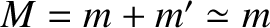 is the total mass of the Earth-Moon system. The Earth (including the oceans) is
treated as a uniform sphere of mass
is the total mass of the Earth-Moon system. The Earth (including the oceans) is
treated as a uniform sphere of mass  , and radius
, and radius  that rotates daily about its axis (which is approximately normal to the
orbital plane of the Moon) at the angular velocity
that rotates daily about its axis (which is approximately normal to the
orbital plane of the Moon) at the angular velocity
 . Note, incidentally, that the Earth rotates in the same sense that the Moon
orbits, as indicated in the figure.
As we saw in the previous section, spatial gradients in the Moon's gravitational field produce a slight tidal elongation
of the Earth. However, because of frictional effects,
this elongation does not quite line up along the axis joining the centers of the Earth and Moon. In fact,
because
. Note, incidentally, that the Earth rotates in the same sense that the Moon
orbits, as indicated in the figure.
As we saw in the previous section, spatial gradients in the Moon's gravitational field produce a slight tidal elongation
of the Earth. However, because of frictional effects,
this elongation does not quite line up along the axis joining the centers of the Earth and Moon. In fact,
because
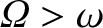 , the tidal elongation is carried ahead (in the sense defined by the Earth's rotation) of this axis by some small angle
, the tidal elongation is carried ahead (in the sense defined by the Earth's rotation) of this axis by some small angle 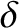 (say),
as shown in the figure.
(say),
as shown in the figure.
Figure 6.10:
Origin of tidal torque.
|
|
Defining a spherical coordinate system, 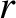 ,
,  ,
, 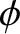 , whose origin is the center of the Earth, and which is
orientated such that the Earth-Moon axis always corresponds to
, whose origin is the center of the Earth, and which is
orientated such that the Earth-Moon axis always corresponds to 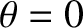 (see Figure 6.7), we find that the Earth's external gravitational potential is [cf., Equation (3.65)]
(see Figure 6.7), we find that the Earth's external gravitational potential is [cf., Equation (3.65)]
![$\displaystyle {\mit\Phi}(r,\theta) = -\frac{G\,m}{r} +\frac{\epsilon}{5}\,\frac{G\,m\,R^{\,2}}{r^{\,3}}
\left[3\,\cos^2(\theta-\delta)-1\right],$](img1280.png) |
(6.88) |
where 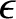 is the ellipticity induced by the tidal field of the Moon.
Note that the second term on the right-hand side of this expression is the contribution of the Earth's tidal bulge, which attains its
maximum amplitude at
is the ellipticity induced by the tidal field of the Moon.
Note that the second term on the right-hand side of this expression is the contribution of the Earth's tidal bulge, which attains its
maximum amplitude at
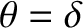 , rather than
, rather than 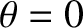 , because of the aforementioned misalignment between the
bulge and the Earth-Moon axis.
Equations (6.76), (6.79), and (6.88) can be combined to give
, because of the aforementioned misalignment between the
bulge and the Earth-Moon axis.
Equations (6.76), (6.79), and (6.88) can be combined to give
![$\displaystyle {\mit\Phi}(r,\theta) = -\frac{G\,m}{r} -\frac{3}{4}\,\frac{G\,m'\...
...})\,r^{\,3}}\left(\frac{R}{a}\right)^3
\left[3\,\cos^2(\theta-\delta)-1\right].$](img1282.png) |
(6.89) |
From Equation (3.7), the torque about the Earth's center that the terrestrial gravitational field exerts on the Moon is
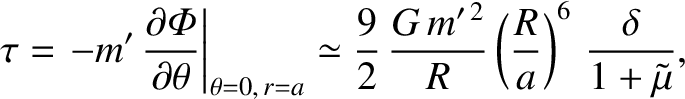 |
(6.90) |
where use has been made of Equation (6.89), as well as the fact that 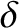 is a small
angle.
There is
zero torque in the absence of
a misalignment between the Earth's tidal bulge and the Earth-Moon axis.
The torque
is a small
angle.
There is
zero torque in the absence of
a misalignment between the Earth's tidal bulge and the Earth-Moon axis.
The torque 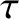 acts to increase the Moon's orbital angular momentum. By conservation of angular
momentum, an equal and opposite torque,
acts to increase the Moon's orbital angular momentum. By conservation of angular
momentum, an equal and opposite torque,  ,
is applied to the Earth; it acts to decrease the terrestrial rotational angular momentum.
Incidentally, if the Moon
were sufficiently close to the Earth that its orbital angular velocity exceeded the Earth's rotational
angular velocity (i.e., if
,
is applied to the Earth; it acts to decrease the terrestrial rotational angular momentum.
Incidentally, if the Moon
were sufficiently close to the Earth that its orbital angular velocity exceeded the Earth's rotational
angular velocity (i.e., if
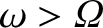 ) then the phase lag between the
Earth's tidal elongation and the Moon's tidal field would cause the tidal bulge to fall slightly behind the Earth-Moon axis (i.e.,
) then the phase lag between the
Earth's tidal elongation and the Moon's tidal field would cause the tidal bulge to fall slightly behind the Earth-Moon axis (i.e., 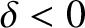 ). In this
case, the gravitational torque would act to reduce the Moon's orbital angular momentum, and to increase the
Earth's rotational angular momentum.
). In this
case, the gravitational torque would act to reduce the Moon's orbital angular momentum, and to increase the
Earth's rotational angular momentum.
The Earth's rotational equation of motion is
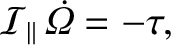 |
(6.91) |
where
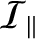 is the moment of inertia about the terrestrial rotation axis. Very crudely approximating the Earth as a uniform
sphere, we have
is the moment of inertia about the terrestrial rotation axis. Very crudely approximating the Earth as a uniform
sphere, we have
 . Hence, the previous two equations can be combined to give
. Hence, the previous two equations can be combined to give
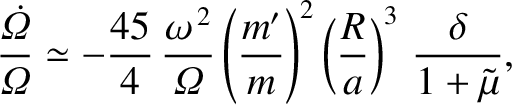 |
(6.92) |
where use has been made of Equation (6.87), as well as the fact that 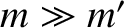 .
Now, a time lag of 12 minutes between the Moon being overhead and a
maximum of the Earth's tidal elongation implies a lag angle of
.
Now, a time lag of 12 minutes between the Moon being overhead and a
maximum of the Earth's tidal elongation implies a lag angle of
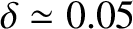 radians (i.e.,
radians (i.e.,
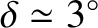 ).
Hence, employing the observed values
).
Hence, employing the observed values
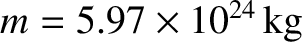 ,
,
 ,
,
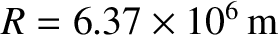 ,
,
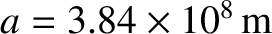 ,
,
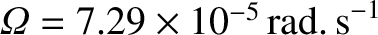 , and
, and
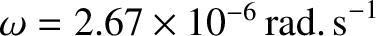 (Yoder 1995),
as well as the estimate
(Yoder 1995),
as well as the estimate
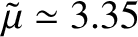 (from the previous section),
we find that
(from the previous section),
we find that
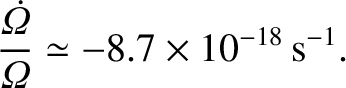 |
(6.93) |
It follows that, under the influence of the tidal torque, the
Earth's axial rotation is gradually decelerating. Indeed, according to this estimate,
the length of a day
should be increasing at the rate of about 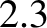 milliseconds per century. Analysis of ancient and medieval
solar and lunar eclipse records indicates that the length of the day is actually increasing at the rate
of
milliseconds per century. Analysis of ancient and medieval
solar and lunar eclipse records indicates that the length of the day is actually increasing at the rate
of 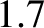 milliseconds per century (Stephenson and Morrison 1995).
The
timescale for the tidal torque to significantly reduce the Earth's rotational angular velocity is estimated to be
milliseconds per century (Stephenson and Morrison 1995).
The
timescale for the tidal torque to significantly reduce the Earth's rotational angular velocity is estimated to be
 |
(6.94) |
This timescale is comparable with the Earth's age, which is thought to be
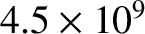 years. Hence,
we conclude that, although the Earth is certainly old enough for the tidal torque to have significantly reduced its rotational
angular velocity, it is plausible that it is not sufficiently old for the torque to have driven the Earth-Moon system to
a final steady state. Such a state, in which the Earth's rotational angular velocity matches the Moon's
orbital angular velocity, is termed synchronous. In a
synchronous state, the Moon would appear stationary to an observer on the Earth's surface, and, hence, there would
be no tides (from the observer's perspective), no phase lag, and no tidal torque.
years. Hence,
we conclude that, although the Earth is certainly old enough for the tidal torque to have significantly reduced its rotational
angular velocity, it is plausible that it is not sufficiently old for the torque to have driven the Earth-Moon system to
a final steady state. Such a state, in which the Earth's rotational angular velocity matches the Moon's
orbital angular velocity, is termed synchronous. In a
synchronous state, the Moon would appear stationary to an observer on the Earth's surface, and, hence, there would
be no tides (from the observer's perspective), no phase lag, and no tidal torque.
Up to now, we have concentrated on the effect of the tidal torque on the rotation of the Earth.
Let us now examine its effect on the orbit of the Moon.
The total angular momentum of the Earth-Moon system is
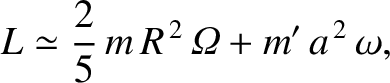 |
(6.95) |
where the first term on the right-hand side is the rotational angular momentum of the Earth, and the
second the orbital angular momentum of the Moon. Of course, 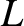 is a conserved quantity. Moreover,
is a conserved quantity. Moreover,
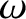 and
and  are related according to Equation (6.87). It follows that
are related according to Equation (6.87). It follows that
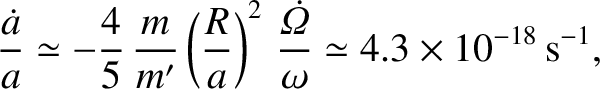 |
(6.96) |
where use has been made of Equation (6.93).
In other words, the tidal torque causes the radius of the Moon's orbit to gradually increase. According to
the previous estimate, this increase should take place at the rate of about
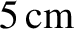 a
year. The observed rate, which is obtained from lunar laser ranging data,
is
a
year. The observed rate, which is obtained from lunar laser ranging data,
is
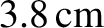 a year (Chapront et al. 2002). This suggests that, despite the numerous approximations that we have made, our calculation remains reasonably accurate.
We also have
a year (Chapront et al. 2002). This suggests that, despite the numerous approximations that we have made, our calculation remains reasonably accurate.
We also have
 |
(6.97) |
In other words, the tidal torque produces a gradual deceleration in the Moon's orbital angular velocity. According to this estimate, the deceleration should take place at the rate of 35 arc seconds per century
squared. The measured deceleration is about 26 arc seconds per century squared (Yoder 1995). (Note that, despite this angular deceleration, the Moon's orbital
angular momentum is actually increasing in time, because its orbital radius is increasing.)
The net rate at which the tidal torques acting on the Moon and the Earth do work is
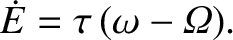 |
(6.98) |
Note that  , because
, because 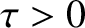 and
and
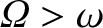 . This implies that the deceleration of the Earth's
rotation and that of the Moon's orbital angular velocity induced by tidal torques are necessarily associated with the
dissipation of energy. This dissipation manifests itself as frictional heating of the Earth's crust and
the oceans (Bertotti et al. 2003).
. This implies that the deceleration of the Earth's
rotation and that of the Moon's orbital angular velocity induced by tidal torques are necessarily associated with the
dissipation of energy. This dissipation manifests itself as frictional heating of the Earth's crust and
the oceans (Bertotti et al. 2003).
Of course, we would expect spatial gradients in the gravitational field of the Earth to generate a tidal bulge in the Moon.
We would also expect dissipative effects to produce a phase lag between this bulge and the Earth. This would allow
the Earth to exert a gravitational torque that acts to drive the Moon toward a synchronous state in which its rotational angular
velocity matches its orbital angular velocity. By analogy with the previous analysis, the de-spinning rate
of the Moon is estimated to be
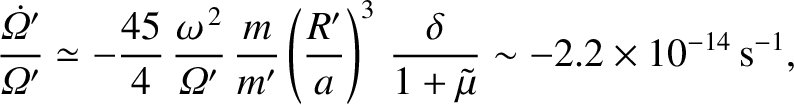 |
(6.99) |
where
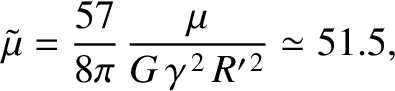 |
(6.100) |
is the Moon's effective rigidity,
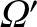 its rotational angular velocity,
its rotational angular velocity,
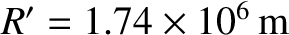 its radius,
its radius,
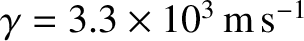 its density (Yoder 1995),
its density (Yoder 1995),
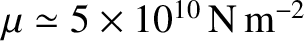 its shear modulus
(Zhang 1992), and
its shear modulus
(Zhang 1992), and 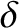 the lag angle.
The preceding numerical estimate is made with the guesses
the lag angle.
The preceding numerical estimate is made with the guesses
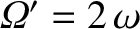 and
and
 radians. Thus, the
time required for the Moon to achieve a synchronous state is
radians. Thus, the
time required for the Moon to achieve a synchronous state is
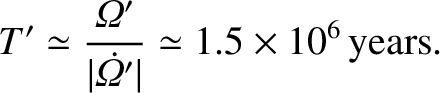 |
(6.101) |
This is considerably less than the age of the Moon. Hence, it is not surprising that the Moon has actually
achieved a synchronous state, as evidenced by the fact that the same side of the Moon is always
visible from the Earth. (See Section 8.11.)
 and which is
treated as a point particle, orbits the Earth (it actually orbits the center of mass of the Earth-Moon system, but this
amounts to almost the same thing) in an approximately circular orbit of radius
and which is
treated as a point particle, orbits the Earth (it actually orbits the center of mass of the Earth-Moon system, but this
amounts to almost the same thing) in an approximately circular orbit of radius  . Moreover, the orbital angular velocity of the
Moon is [see Equation (6.59)]
where
. Moreover, the orbital angular velocity of the
Moon is [see Equation (6.59)]
where
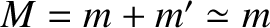 is the total mass of the Earth-Moon system. The Earth (including the oceans) is
treated as a uniform sphere of mass
is the total mass of the Earth-Moon system. The Earth (including the oceans) is
treated as a uniform sphere of mass  , and radius
, and radius 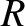 that rotates daily about its axis (which is approximately normal to the
orbital plane of the Moon) at the angular velocity
that rotates daily about its axis (which is approximately normal to the
orbital plane of the Moon) at the angular velocity
 . Note, incidentally, that the Earth rotates in the same sense that the Moon
orbits, as indicated in the figure.
As we saw in the previous section, spatial gradients in the Moon's gravitational field produce a slight tidal elongation
of the Earth. However, because of frictional effects,
this elongation does not quite line up along the axis joining the centers of the Earth and Moon. In fact,
because
. Note, incidentally, that the Earth rotates in the same sense that the Moon
orbits, as indicated in the figure.
As we saw in the previous section, spatial gradients in the Moon's gravitational field produce a slight tidal elongation
of the Earth. However, because of frictional effects,
this elongation does not quite line up along the axis joining the centers of the Earth and Moon. In fact,
because
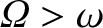 , the tidal elongation is carried ahead (in the sense defined by the Earth's rotation) of this axis by some small angle
, the tidal elongation is carried ahead (in the sense defined by the Earth's rotation) of this axis by some small angle 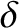 (say),
as shown in the figure.
(say),
as shown in the figure.
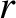 ,
,  ,
, 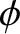 , whose origin is the center of the Earth, and which is
orientated such that the Earth-Moon axis always corresponds to
, whose origin is the center of the Earth, and which is
orientated such that the Earth-Moon axis always corresponds to 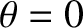 (see Figure 6.7), we find that the Earth's external gravitational potential is [cf., Equation (3.65)]
(see Figure 6.7), we find that the Earth's external gravitational potential is [cf., Equation (3.65)]
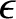 is the ellipticity induced by the tidal field of the Moon.
Note that the second term on the right-hand side of this expression is the contribution of the Earth's tidal bulge, which attains its
maximum amplitude at
is the ellipticity induced by the tidal field of the Moon.
Note that the second term on the right-hand side of this expression is the contribution of the Earth's tidal bulge, which attains its
maximum amplitude at
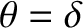 , rather than
, rather than 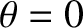 , because of the aforementioned misalignment between the
bulge and the Earth-Moon axis.
Equations (6.76), (6.79), and (6.88) can be combined to give
, because of the aforementioned misalignment between the
bulge and the Earth-Moon axis.
Equations (6.76), (6.79), and (6.88) can be combined to give
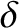 is a small
angle.
There is
zero torque in the absence of
a misalignment between the Earth's tidal bulge and the Earth-Moon axis.
The torque
is a small
angle.
There is
zero torque in the absence of
a misalignment between the Earth's tidal bulge and the Earth-Moon axis.
The torque 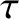 acts to increase the Moon's orbital angular momentum. By conservation of angular
momentum, an equal and opposite torque,
acts to increase the Moon's orbital angular momentum. By conservation of angular
momentum, an equal and opposite torque,  ,
is applied to the Earth; it acts to decrease the terrestrial rotational angular momentum.
Incidentally, if the Moon
were sufficiently close to the Earth that its orbital angular velocity exceeded the Earth's rotational
angular velocity (i.e., if
,
is applied to the Earth; it acts to decrease the terrestrial rotational angular momentum.
Incidentally, if the Moon
were sufficiently close to the Earth that its orbital angular velocity exceeded the Earth's rotational
angular velocity (i.e., if
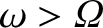 ) then the phase lag between the
Earth's tidal elongation and the Moon's tidal field would cause the tidal bulge to fall slightly behind the Earth-Moon axis (i.e.,
) then the phase lag between the
Earth's tidal elongation and the Moon's tidal field would cause the tidal bulge to fall slightly behind the Earth-Moon axis (i.e., 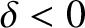 ). In this
case, the gravitational torque would act to reduce the Moon's orbital angular momentum, and to increase the
Earth's rotational angular momentum.
). In this
case, the gravitational torque would act to reduce the Moon's orbital angular momentum, and to increase the
Earth's rotational angular momentum.
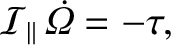
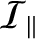 is the moment of inertia about the terrestrial rotation axis. Very crudely approximating the Earth as a uniform
sphere, we have
is the moment of inertia about the terrestrial rotation axis. Very crudely approximating the Earth as a uniform
sphere, we have
 . Hence, the previous two equations can be combined to give
. Hence, the previous two equations can be combined to give
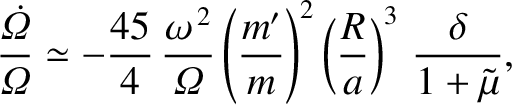
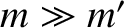 .
Now, a time lag of 12 minutes between the Moon being overhead and a
maximum of the Earth's tidal elongation implies a lag angle of
.
Now, a time lag of 12 minutes between the Moon being overhead and a
maximum of the Earth's tidal elongation implies a lag angle of
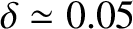 radians (i.e.,
radians (i.e.,
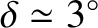 ).
Hence, employing the observed values
).
Hence, employing the observed values
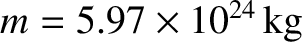 ,
,
 ,
,
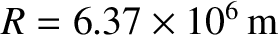 ,
,
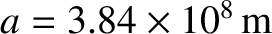 ,
,
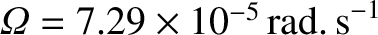 , and
, and
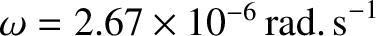 (Yoder 1995),
as well as the estimate
(Yoder 1995),
as well as the estimate
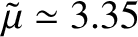 (from the previous section),
we find that
It follows that, under the influence of the tidal torque, the
Earth's axial rotation is gradually decelerating. Indeed, according to this estimate,
the length of a day
should be increasing at the rate of about
(from the previous section),
we find that
It follows that, under the influence of the tidal torque, the
Earth's axial rotation is gradually decelerating. Indeed, according to this estimate,
the length of a day
should be increasing at the rate of about 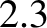 milliseconds per century. Analysis of ancient and medieval
solar and lunar eclipse records indicates that the length of the day is actually increasing at the rate
of
milliseconds per century. Analysis of ancient and medieval
solar and lunar eclipse records indicates that the length of the day is actually increasing at the rate
of 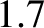 milliseconds per century (Stephenson and Morrison 1995).
The
timescale for the tidal torque to significantly reduce the Earth's rotational angular velocity is estimated to be
milliseconds per century (Stephenson and Morrison 1995).
The
timescale for the tidal torque to significantly reduce the Earth's rotational angular velocity is estimated to be

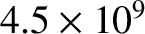 years. Hence,
we conclude that, although the Earth is certainly old enough for the tidal torque to have significantly reduced its rotational
angular velocity, it is plausible that it is not sufficiently old for the torque to have driven the Earth-Moon system to
a final steady state. Such a state, in which the Earth's rotational angular velocity matches the Moon's
orbital angular velocity, is termed synchronous. In a
synchronous state, the Moon would appear stationary to an observer on the Earth's surface, and, hence, there would
be no tides (from the observer's perspective), no phase lag, and no tidal torque.
years. Hence,
we conclude that, although the Earth is certainly old enough for the tidal torque to have significantly reduced its rotational
angular velocity, it is plausible that it is not sufficiently old for the torque to have driven the Earth-Moon system to
a final steady state. Such a state, in which the Earth's rotational angular velocity matches the Moon's
orbital angular velocity, is termed synchronous. In a
synchronous state, the Moon would appear stationary to an observer on the Earth's surface, and, hence, there would
be no tides (from the observer's perspective), no phase lag, and no tidal torque.
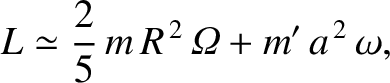
 is a conserved quantity. Moreover,
is a conserved quantity. Moreover,
 and
and  are related according to Equation (6.87). It follows that
are related according to Equation (6.87). It follows that
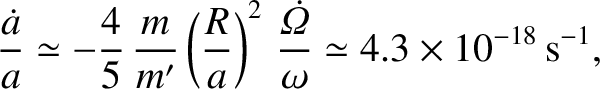
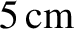 a
year. The observed rate, which is obtained from lunar laser ranging data,
is
a
year. The observed rate, which is obtained from lunar laser ranging data,
is
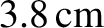 a year (Chapront et al. 2002). This suggests that, despite the numerous approximations that we have made, our calculation remains reasonably accurate.
We also have
a year (Chapront et al. 2002). This suggests that, despite the numerous approximations that we have made, our calculation remains reasonably accurate.
We also have

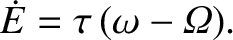
 , because
, because 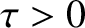 and
and
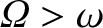 . This implies that the deceleration of the Earth's
rotation and that of the Moon's orbital angular velocity induced by tidal torques are necessarily associated with the
dissipation of energy. This dissipation manifests itself as frictional heating of the Earth's crust and
the oceans (Bertotti et al. 2003).
. This implies that the deceleration of the Earth's
rotation and that of the Moon's orbital angular velocity induced by tidal torques are necessarily associated with the
dissipation of energy. This dissipation manifests itself as frictional heating of the Earth's crust and
the oceans (Bertotti et al. 2003).
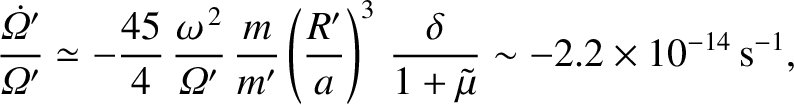
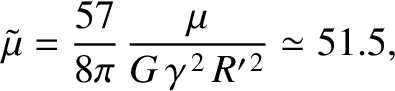
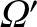 its rotational angular velocity,
its rotational angular velocity,
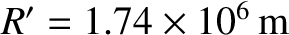 its radius,
its radius,
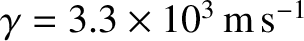 its density (Yoder 1995),
its density (Yoder 1995),
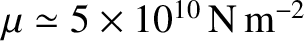 its shear modulus
(Zhang 1992), and
its shear modulus
(Zhang 1992), and 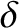 the lag angle.
The preceding numerical estimate is made with the guesses
the lag angle.
The preceding numerical estimate is made with the guesses
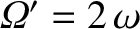 and
and
 radians. Thus, the
time required for the Moon to achieve a synchronous state is
radians. Thus, the
time required for the Moon to achieve a synchronous state is