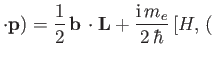

Next: Magnetic Dipole Transitions
Up: Time-Dependent Perturbation Theory
Previous: Electric Dipole Transitions
We saw in Section 8.10 that a spontaneous electromagnetic transition between some initial atomic state,  , and some final state,
, and some final state,  ,
is mediated by the matrix element
,
is mediated by the matrix element
 ![$\displaystyle \cdot{\bf d}_{if} = \frac{-{\rm i}}{m_e\,\omega_{if}}\left\langle...
...\bf x}\right]\mbox{\boldmath$\epsilon$}\cdot{\bf p} \right\vert f\right\rangle.$](img2627.png) |
(8.183) |
Now,
![$\displaystyle \exp\left[\,{\rm i}\left(\frac{\omega}{c}\right){\bf n}\cdot{\bf x}\right] = 1 + {\rm i}\,\frac{\omega}{c} \,{\bf n}\cdot{\bf x} + \cdots.$](img2628.png) |
(8.184) |
However, as explained in the previous section, the fact that the wavelength of the
radiation that is emitted during spontaneous transition
is generally much larger than the
typical size of
the atom allows us to truncated the previous expansion.
Retaining the first two terms,
we obtain
where use has been made of Equation (8.170). Moreover, we
have assumed that
 (i.e., the angular frequency of the electromagnetic radiation
matches that associated with the atomic transition.) Suppose, however, that the transition from state
(i.e., the angular frequency of the electromagnetic radiation
matches that associated with the atomic transition.) Suppose, however, that the transition from state 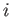 to
state
to
state 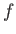 is forbidden according to the selection rules for electric dipole transitions. This implies that
is forbidden according to the selection rules for electric dipole transitions. This implies that
In this case, Equation (8.188) reduces to
We deduce that a ``forbidden'' transition is not, strictly speaking, forbidden [i.e., Equation (8.189) does not
necessarily mean that
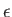
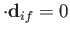 ], but rather takes place at
a significantly lower rate than an electric dipole transition [because, according to the previous expression,
], but rather takes place at
a significantly lower rate than an electric dipole transition [because, according to the previous expression,
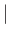
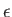
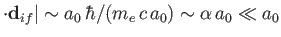 , whereas
, whereas
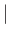
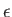
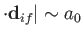 for an electric dipole transition (see Section 8.11)].
for an electric dipole transition (see Section 8.11)].
According to classical electromagnetic theory, the polarization direction of the magnetic component of an electromagnetic wave propagating in the
direction 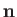 is given by
is given by
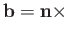
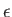 , where
, where
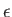 specifies the direction of the
wave's electric component [49]. Of course,
specifies the direction of the
wave's electric component [49]. Of course,
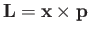 represents orbital
angular momentum. However,
represents orbital
angular momentum. However,
Furthermore, if
then
Here, use has been made of Equations (3.32) and (3.33), as well as the fact that
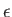
 .
It follows, from the previous three equations, that
.
It follows, from the previous three equations, that
Hence, Equation (8.190) yields
where
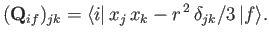 |
(8.193) |
Here,
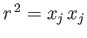 . Moreover, we have made use of the fact that
. Moreover, we have made use of the fact that
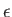
 to write
to write
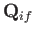 as a traceless tensor.
In the following, we shall treat the two terms on the right-hand side of Equation (8.195) separately, because
they give rise to completely different selection rules. The first term governs so-called magnetic dipole transitions,
whereas the second governs so-called electric quadrupole transitions.
as a traceless tensor.
In the following, we shall treat the two terms on the right-hand side of Equation (8.195) separately, because
they give rise to completely different selection rules. The first term governs so-called magnetic dipole transitions,
whereas the second governs so-called electric quadrupole transitions.


Next: Magnetic Dipole Transitions
Up: Time-Dependent Perturbation Theory
Previous: Electric Dipole Transitions
Richard Fitzpatrick
2016-01-22
![$\displaystyle \cdot{\bf d}_{if} = \frac{-{\rm i}}{m_e\,\omega_{if}}\left\langle...
...\bf x}\right]\mbox{\boldmath$\epsilon$}\cdot{\bf p} \right\vert f\right\rangle.$](img2627.png)
![$\displaystyle \cdot{\bf d}_{if} = \frac{-{\rm i}}{m_e\,\omega_{if}}\left\langle...
...\bf x}\right]\mbox{\boldmath$\epsilon$}\cdot{\bf p} \right\vert f\right\rangle.$](img2627.png)
![$\displaystyle \exp\left[\,{\rm i}\left(\frac{\omega}{c}\right){\bf n}\cdot{\bf x}\right] = 1 + {\rm i}\,\frac{\omega}{c} \,{\bf n}\cdot{\bf x} + \cdots.$](img2628.png)
![]() is given by
is given by
![]()
![]() , where
, where
![]() specifies the direction of the
wave's electric component [49]. Of course,
specifies the direction of the
wave's electric component [49]. Of course,
![]() represents orbital
angular momentum. However,
represents orbital
angular momentum. However,
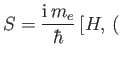
![$\displaystyle = \frac{{\rm i}\,m_e}{\hbar}\,\epsilon_i\,n_j\,[H,\,x_i\,x_j] = \...
...{\rm i}\,m_e}{\hbar}\,\epsilon_i\,n_j\left(x_i\,[H,\,x_j]+[H,\,x_i]\,x_j\right)$](img2649.png)