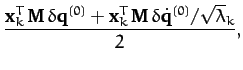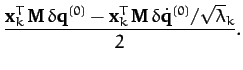Next: Normal Coordinates
Up: Coupled Oscillations
Previous: More Matrix Eigenvalue Theory
It follows from Equation (783) and (784), plus the
mathematical results contained in the previous section, that the
most general solution to Equation (782) can be written
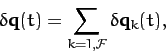 |
(800) |
where
 |
(801) |
Here, the  and the
and the 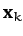 are the eigenvalues and eigenvectors obtained by solving Equation (786). Moreover, the
are the eigenvalues and eigenvectors obtained by solving Equation (786). Moreover, the 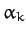 and
and  are arbitrary constants. Finally, we have made
use of the fact that the two roots of
are arbitrary constants. Finally, we have made
use of the fact that the two roots of
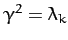 are
are
 .
.
According to Equation (800), the most general perturbed motion of the
system consists of a linear combination of 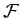 different modes. These
modes are generally termed normal modes, since they are mutually
orthogonal (because the
different modes. These
modes are generally termed normal modes, since they are mutually
orthogonal (because the 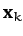 are mutually orthogonal). Furthermore, it follows
from the independence of the
are mutually orthogonal). Furthermore, it follows
from the independence of the 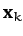 that the normal
modes are also independent (i.e., one mode cannot be expressed as a
linear combination of the others). The
that the normal
modes are also independent (i.e., one mode cannot be expressed as a
linear combination of the others). The 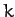 th normal mode has a specific
pattern of motion which is specified by the
th normal mode has a specific
pattern of motion which is specified by the 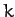 th eigenvector,
th eigenvector, 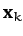 .
Moreover, the
.
Moreover, the 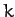 th mode has a specific time variation which is determined by the associated eigenvalue,
th mode has a specific time variation which is determined by the associated eigenvalue,  . Recall that
. Recall that
 is real. Hence, there are only two possibilities. Either
is real. Hence, there are only two possibilities. Either  is positive, in which case we can write
is positive, in which case we can write
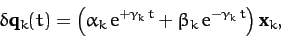 |
(802) |
where
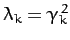 , or
, or
 is negative, in which case we can write
is negative, in which case we can write
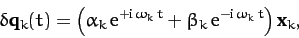 |
(803) |
where
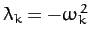 . In other words, if
. In other words, if  is
positive then the
is
positive then the 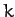 th normal mode grows or decays secularly in time, whereas
if
th normal mode grows or decays secularly in time, whereas
if  is negative then the
is negative then the 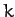 th normal mode oscillates in time.
Obviously, if the system possesses one or more normal modes which grow
secularly in time then the equilibrium about which we originally expanded the
equations of motion must be an unstable equilibrium. On the
other hand, if all of the normal modes oscillate in time then the equilibrium is
stable. Thus, we conclude that whilst Equation (773)
is the condition for the existence of an equilibrium state in a many degree of freedom system, the condition for the
equilibrium to be stable is that all of the eigenvalues of the stability
equation (786) must be negative.
th normal mode oscillates in time.
Obviously, if the system possesses one or more normal modes which grow
secularly in time then the equilibrium about which we originally expanded the
equations of motion must be an unstable equilibrium. On the
other hand, if all of the normal modes oscillate in time then the equilibrium is
stable. Thus, we conclude that whilst Equation (773)
is the condition for the existence of an equilibrium state in a many degree of freedom system, the condition for the
equilibrium to be stable is that all of the eigenvalues of the stability
equation (786) must be negative.
The arbitrary constants 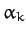 and
and  appearing in expression (801)
are determined from the initial conditions. Thus, if
appearing in expression (801)
are determined from the initial conditions. Thus, if
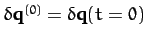 and
and
 then it is easily demonstrated from Equations (799)-(801)
that
then it is easily demonstrated from Equations (799)-(801)
that
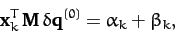 |
(804) |
and
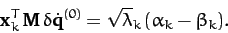 |
(805) |
Hence,
Note, finally, that since there are 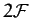 arbitrary constants (two for each of the
arbitrary constants (two for each of the 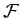 normal modes), we can be sure that Equation (800) represents the
most general solution to Equation (782).
normal modes), we can be sure that Equation (800) represents the
most general solution to Equation (782).



Next: Normal Coordinates
Up: Coupled Oscillations
Previous: More Matrix Eigenvalue Theory
Richard Fitzpatrick
2011-03-31
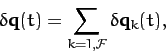
![]() different modes. These
modes are generally termed normal modes, since they are mutually
orthogonal (because the
different modes. These
modes are generally termed normal modes, since they are mutually
orthogonal (because the ![]() are mutually orthogonal). Furthermore, it follows
from the independence of the
are mutually orthogonal). Furthermore, it follows
from the independence of the ![]() that the normal
modes are also independent (i.e., one mode cannot be expressed as a
linear combination of the others). The
that the normal
modes are also independent (i.e., one mode cannot be expressed as a
linear combination of the others). The ![]() th normal mode has a specific
pattern of motion which is specified by the
th normal mode has a specific
pattern of motion which is specified by the ![]() th eigenvector,
th eigenvector, ![]() .
Moreover, the
.
Moreover, the ![]() th mode has a specific time variation which is determined by the associated eigenvalue,
th mode has a specific time variation which is determined by the associated eigenvalue, ![]() . Recall that
. Recall that
![]() is real. Hence, there are only two possibilities. Either
is real. Hence, there are only two possibilities. Either ![]() is positive, in which case we can write
is positive, in which case we can write
![]() and
and ![]() appearing in expression (801)
are determined from the initial conditions. Thus, if
appearing in expression (801)
are determined from the initial conditions. Thus, if
![]() and
and
![]() then it is easily demonstrated from Equations (799)-(801)
that
then it is easily demonstrated from Equations (799)-(801)
that