


Next: More Matrix Eigenvalue Theory
Up: Coupled Oscillations
Previous: Equilibrium State
It is evident that if our system is initialized in some equilibrium state, with
all of the 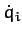 set to zero, then it will remain in this state for ever.
But what happens if the system is slightly perturbed from the equilibrium
state?
set to zero, then it will remain in this state for ever.
But what happens if the system is slightly perturbed from the equilibrium
state?
Let
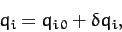 |
(774) |
for 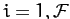 , where the
, where the  are small. To lowest order in
are small. To lowest order in  , the
kinetic energy (770) can be written
, the
kinetic energy (770) can be written
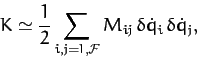 |
(775) |
where
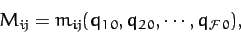 |
(776) |
and
 |
(777) |
Note that the weights  in the quadratic form (775) are now constants.
in the quadratic form (775) are now constants.
Taylor expanding the potential energy function about the equilibrium state, up to second-order in the  , we obtain
, we obtain
 |
(778) |
where
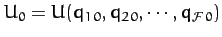 , the
, the 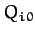 are specified in Equation (773), and
are specified in Equation (773), and
 |
(779) |
Now, we can set 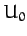 to zero without loss of generality. Moreover, according to Equation (773), the
to zero without loss of generality. Moreover, according to Equation (773), the
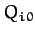 are all zero. Hence, the expression (778) reduces to
are all zero. Hence, the expression (778) reduces to
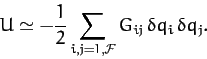 |
(780) |
Note that, since
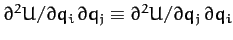 , the constants weights
, the constants weights 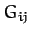 in the
above quadratic form are invariant under interchange of the indices
in the
above quadratic form are invariant under interchange of the indices 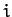 and
and 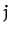 : i.e.,
: i.e.,
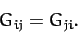 |
(781) |
With 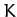 and
and 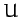 specified by the quadratic forms (775) and (780), respectively, Lagrange's equations of motion (772) reduce to
specified by the quadratic forms (775) and (780), respectively, Lagrange's equations of motion (772) reduce to
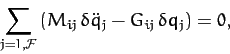 |
(782) |
for 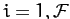 .
Note that the above coupled differential equations are linear in the
.
Note that the above coupled differential equations are linear in the  . It follows
that the solutions are superposable.
Let us search for solutions of the above equations in which all of the perturbed coordinates
. It follows
that the solutions are superposable.
Let us search for solutions of the above equations in which all of the perturbed coordinates  have a common time variation of the form
have a common time variation of the form
 |
(783) |
for 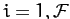 .
Now, Equations (782) are a set of
.
Now, Equations (782) are a set of 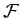 second-order differential equations.
Hence, the most general solution contains
second-order differential equations.
Hence, the most general solution contains 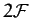 arbitrary constants of integration. Thus, if we can find sufficient independent solutions of the form (783) to Equations (782) that the superposition
of these solutions contains
arbitrary constants of integration. Thus, if we can find sufficient independent solutions of the form (783) to Equations (782) that the superposition
of these solutions contains 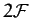 arbitrary constants then we can be sure that we
have found the most general solution. Equations
(782) and (783) yield
arbitrary constants then we can be sure that we
have found the most general solution. Equations
(782) and (783) yield
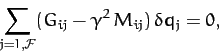 |
(784) |
which can be written more succinctly as a matrix equation:
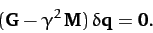 |
(785) |
Here,  is the real [see Equation (779)] symmetric [see Equation (781)]
is the real [see Equation (779)] symmetric [see Equation (781)]
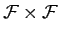 matrix of the
matrix of the 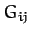 values.
Furthermore,
values.
Furthermore, 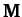 is the real [see Equation (770)] symmetric [see Equation (777)]
is the real [see Equation (770)] symmetric [see Equation (777)]
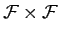 matrix of the
matrix of the  values. Finally,
values. Finally,
 is the
is the
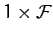 vector of the
vector of the  values, and
values, and
 is a null vector.
is a null vector.



Next: More Matrix Eigenvalue Theory
Up: Coupled Oscillations
Previous: Equilibrium State
Richard Fitzpatrick
2011-03-31
![]() , we obtain
, we obtain
![]() and
and ![]() specified by the quadratic forms (775) and (780), respectively, Lagrange's equations of motion (772) reduce to
specified by the quadratic forms (775) and (780), respectively, Lagrange's equations of motion (772) reduce to