


Next: Eulerian Angles
Up: Rigid Body Rotation
Previous: Principal Axes of Rotation
The fundamental equation of motion of a rotating body [see Equation (456)],
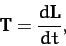 |
(501) |
is only valid in an inertial frame. However, we have seen that 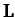 is most simply expressed in a frame of reference whose axes are aligned
along the principal axes of rotation of the body. Such a frame of reference
rotates with the body, and is, therefore, non-inertial. Thus, it is helpful to define two Cartesian coordinate systems, with the same origins. The first,
with coordinates
is most simply expressed in a frame of reference whose axes are aligned
along the principal axes of rotation of the body. Such a frame of reference
rotates with the body, and is, therefore, non-inertial. Thus, it is helpful to define two Cartesian coordinate systems, with the same origins. The first,
with coordinates  ,
,  ,
,  , is a fixed inertial frame--let us denote
this the fixed frame. The second, with coordinates
, is a fixed inertial frame--let us denote
this the fixed frame. The second, with coordinates 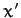 ,
, 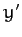 ,
, 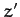 ,
co-rotates with the body in such a manner that the
,
co-rotates with the body in such a manner that the 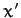 -,
-, 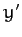 -, and
-, and 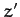 -axes are always pointing along its principal axes of rotation--we shall
refer to this as the body frame. Since the body frame co-rotates with the body, its instantaneous angular velocity is the same as that of the
body. Hence, it follows from the analysis in Section 7.2 that
-axes are always pointing along its principal axes of rotation--we shall
refer to this as the body frame. Since the body frame co-rotates with the body, its instantaneous angular velocity is the same as that of the
body. Hence, it follows from the analysis in Section 7.2 that
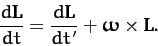 |
(502) |
Here,  is the time derivative in the fixed frame, and
is the time derivative in the fixed frame, and 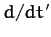 the
time derivative in the body frame.
Combining Equations (501) and (502), we obtain
the
time derivative in the body frame.
Combining Equations (501) and (502), we obtain
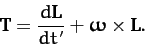 |
(503) |
Now, in the body frame let
 and
and
 .
It follows that
.
It follows that
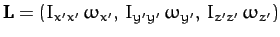 ,
where
,
where 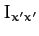 ,
, 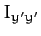 and
and 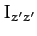 are the principal
moments of inertia. Hence, in the body frame, the components of Equation (503) yield
are the principal
moments of inertia. Hence, in the body frame, the components of Equation (503) yield
where 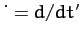 .
Here, we have made use of the fact that the moments of inertia
of a rigid body are constant in time in the co-rotating body frame.
The above equations are known as Euler's equations.
.
Here, we have made use of the fact that the moments of inertia
of a rigid body are constant in time in the co-rotating body frame.
The above equations are known as Euler's equations.
Consider a rigid body which is constrained to rotate about a fixed
axis with constant angular velocity. It follows that
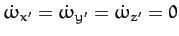 .
Hence, Euler's equations, (504)-(506), reduce to
.
Hence, Euler's equations, (504)-(506), reduce to
These equations specify the components of the steady (in the body frame) torque exerted on the body by
the constraining supports. The steady (in the
body frame) angular momentum is written
 |
(510) |
It is easily demonstrated that
 . Hence,
the torque is perpendicular to both the angular velocity and the angular
momentum vectors.
Note that if the axis of rotation is a principal
axis then two of the three components of
. Hence,
the torque is perpendicular to both the angular velocity and the angular
momentum vectors.
Note that if the axis of rotation is a principal
axis then two of the three components of
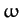 are zero (in the body frame). It follows from Equations (507)-(509) that
all three components of the torque are zero. In other words, zero external torque
is required to make the body rotate steadily about a principal axis.
are zero (in the body frame). It follows from Equations (507)-(509) that
all three components of the torque are zero. In other words, zero external torque
is required to make the body rotate steadily about a principal axis.
Suppose that the body is freely rotating: i.e., there are no external
torques. Furthermore, let the body be rotationally symmetric
about the 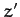 -axis. It follows that
-axis. It follows that
 .
Likewise, we can write
.
Likewise, we can write
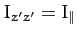 . In general, however,
. In general, however,
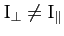 . Thus, Euler's equations yield
. Thus, Euler's equations yield
Clearly,  is a constant of the motion.
Equation (511) and (512) can be written
is a constant of the motion.
Equation (511) and (512) can be written
where
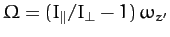 . As is easily
demonstrated, the solution to the above equations is
. As is easily
demonstrated, the solution to the above equations is
where  is a constant. Thus, the projection of the
angular velocity vector onto the
is a constant. Thus, the projection of the
angular velocity vector onto the 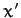 -
-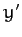 plane has the fixed length
plane has the fixed length
 , and rotates steadily about the
, and rotates steadily about the 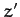 -axis with angular
velocity
-axis with angular
velocity 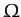 .
It follows that the length of the angular
velocity vector,
.
It follows that the length of the angular
velocity vector,
 , is a constant of the motion.
Clearly, the angular
velocity vector makes some constant angle,
, is a constant of the motion.
Clearly, the angular
velocity vector makes some constant angle, 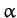 , with the
, with the 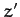 -axis, which implies that
-axis, which implies that
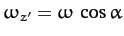 and
and
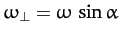 .
Hence, the components of the angular velocity vector are
.
Hence, the components of the angular velocity vector are
where
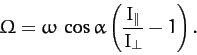 |
(521) |
We conclude that, in the body frame, the angular velocity vector precesses about the
symmetry axis (i.e., the 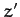 -axis) with the angular
frequency
-axis) with the angular
frequency 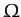 . Now, the components of the angular momentum vector are
. Now, the components of the angular momentum vector are
Thus, in the body frame, the angular momentum vector is also of constant length, and
precesses about the symmetry axis with the angular frequency
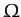 . Furthermore, the angular momentum vector makes a constant angle
. Furthermore, the angular momentum vector makes a constant angle  with the symmetry
axis, where
with the symmetry
axis, where
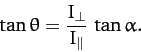 |
(525) |
Note that the angular momentum vector, the angular velocity vector, and
the symmetry axis all lie in the same plane:
i.e.,
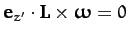 ,
as can easily be verified. Moreover, the
angular momentum vector lies between the angular velocity vector and
the symmetry axis (i.e.,
,
as can easily be verified. Moreover, the
angular momentum vector lies between the angular velocity vector and
the symmetry axis (i.e., 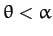 ) for a flattened (or oblate) body
(i.e.,
) for a flattened (or oblate) body
(i.e.,
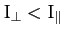 ), whereas the angular velocity vector lies
between the angular momentum vector and the symmetry axis (i.e.,
), whereas the angular velocity vector lies
between the angular momentum vector and the symmetry axis (i.e.,  ) for an elongated (or prolate) body (i.e.,
) for an elongated (or prolate) body (i.e.,
 ).
).
Let us now consider the most general motion of a freely rotating
asymmetric rigid body, as seen in the body frame. Since a freely rotating
body experiences no external torques, its angular momentum vector
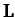 is a constant of the motion in the inertial fixed frame. In general, the direction of this vector varies with time in the non-inertial body frame, but its
length remains fixed. This can be seen from Equation (502):
if
is a constant of the motion in the inertial fixed frame. In general, the direction of this vector varies with time in the non-inertial body frame, but its
length remains fixed. This can be seen from Equation (502):
if 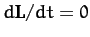 then the scalar product of this equation
with
then the scalar product of this equation
with 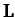 implies that
implies that 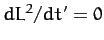 . It follows from Equation (510) that
. It follows from Equation (510) that
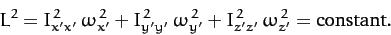 |
(526) |
The above constraint can also be derived directly from Euler's equations,
(504)-(506), by setting
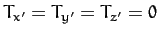 .
A freely rotating body subject to no external torques clearly has a constant rotational kinetic energy.
Hence, from Equation (469),
.
A freely rotating body subject to no external torques clearly has a constant rotational kinetic energy.
Hence, from Equation (469),
 |
(527) |
This constraint can also be derived directly from Euler's equations.
We conclude that, in the body frame, the components of
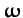 must
simultaneously satisfy the two constraints (526) and (527).
These constraints are the equations of two ellipsoids whose principal
axes coincide with the principal axes of the body, and whose principal
radii are in the ratio
must
simultaneously satisfy the two constraints (526) and (527).
These constraints are the equations of two ellipsoids whose principal
axes coincide with the principal axes of the body, and whose principal
radii are in the ratio
 and
and
 , respectively.
In general, the intersection of these two ellipsoids is a closed curve.
Hence, we conclude that the most general motion of a freely rotating
asymmetric body, as seen in the body frame, is a form of irregular
precession in which the tip of the angular
velocity vector
, respectively.
In general, the intersection of these two ellipsoids is a closed curve.
Hence, we conclude that the most general motion of a freely rotating
asymmetric body, as seen in the body frame, is a form of irregular
precession in which the tip of the angular
velocity vector
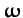 periodically traces out the aforementioned closed curve. It is easily demonstrated that the tip of the angular momentum vector
periodically traces out the aforementioned closed curve. It is easily demonstrated that the tip of the angular momentum vector 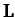 periodically traces out a different closed curve.
periodically traces out a different closed curve.



Next: Eulerian Angles
Up: Rigid Body Rotation
Previous: Principal Axes of Rotation
Richard Fitzpatrick
2011-03-31
![]() .
Hence, Euler's equations, (504)-(506), reduce to
.
Hence, Euler's equations, (504)-(506), reduce to
![]() -axis. It follows that
-axis. It follows that
![]() .
Likewise, we can write
.
Likewise, we can write
![]() . In general, however,
. In general, however,
![]() . Thus, Euler's equations yield
. Thus, Euler's equations yield
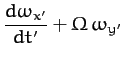

![]() is a constant of the motion in the inertial fixed frame. In general, the direction of this vector varies with time in the non-inertial body frame, but its
length remains fixed. This can be seen from Equation (502):
if
is a constant of the motion in the inertial fixed frame. In general, the direction of this vector varies with time in the non-inertial body frame, but its
length remains fixed. This can be seen from Equation (502):
if ![]() then the scalar product of this equation
with
then the scalar product of this equation
with ![]() implies that
implies that ![]() . It follows from Equation (510) that
. It follows from Equation (510) that