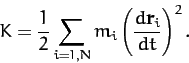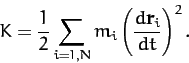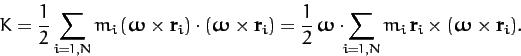Next: Matrix Eigenvalue Theory Up: Rigid Body Rotation Previous: Moment of Inertia Tensor

Rotational Kinetic Energy

The instantaneous rotational kinetic energy of a rotating rigid body is written

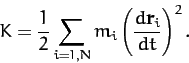$\begin{displaymath} K = \frac{1}{2}\sum_{i=1,N} m_i\left(\frac{d{\bf r}_i}{dt}\right)^2. \end{displaymath}$

(467)

Making use of Equation (457), and some vector identities (see Section A.9), the kinetic energy takes the form

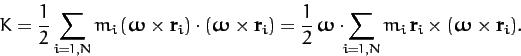$\begin{displaymath} K = \frac{1}{2}\sum_{i=1,N} m_i\,(\mbox{\boldmath$\omega$}\t... ...i\,{\bf r}_i\times (\mbox{\boldmath$\omega$}\times {\bf r}_i). \end{displaymath}$

(468)

Hence, it follows from (458) that

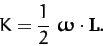$\begin{displaymath} K = \frac{1}{2}\,\, \mbox{\boldmath$\omega$} \cdot {\bf L}. \end{displaymath}$

(469)

Making use of Equation (466), we can also write

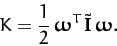$\begin{displaymath} K = \frac{1}{2}\,\mbox{\boldmath$\omega$}^T\,\tilde{\bf I}\,\mbox{\boldmath$\omega$}. \end{displaymath}$

(470)

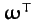Here, $\mbox{\boldmath$\omega$}^T$ is the row vector of the Cartesian components 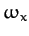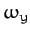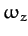$\omega_x$ , $\omega_y$ , $\omega_z$ , which is, of course, the transpose (denoted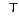

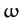) of the column vector $\omega$ . When written in component form, the above equation yields

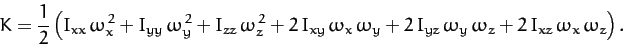$\begin{displaymath} K = \frac{1}{2}\left(I_{xx}\,\omega_x^{\,2}+ I_{yy}\,\omega_... ...z}\,\omega_y\,\omega_z + 2\,I_{xz}\,\omega_x\,\omega_z\right). \end{displaymath}$

(471)

Richard Fitzpatrick 2011-03-31