


Next: Two-Dimensional Sources and Sinks
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Velocity Potentials and Stream
Two-Dimensional Uniform Flow
Consider a steady two-dimensional flow pattern that is uniform: in other words, a pattern which is such that the fluid velocity
is the same everywhere in the  -
- plane. For instance, suppose that the common fluid velocity is
plane. For instance, suppose that the common fluid velocity is
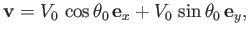 |
(5.27) |
which corresponds to flow at the uniform speed 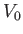 in a fixed direction that subtends a (counter-clockwise) angle
in a fixed direction that subtends a (counter-clockwise) angle
 with the
with the  -axis. It follows, from Equations (5.5) and (5.6), that the
stream function for steady uniform flow takes the form
-axis. It follows, from Equations (5.5) and (5.6), that the
stream function for steady uniform flow takes the form
 |
(5.28) |
When written in terms of cylindrical coordinates, this becomes
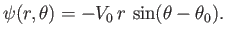 |
(5.29) |
Note, from Equation (5.28), that
 . Thus, it
follows from Equation (5.10) that uniform flow is irrotational. Hence, according to
Section 4.15, such flow can also be derived from a velocity potential. In fact, it is easily
demonstrated that
. Thus, it
follows from Equation (5.10) that uniform flow is irrotational. Hence, according to
Section 4.15, such flow can also be derived from a velocity potential. In fact, it is easily
demonstrated that
 |
(5.30) |



Next: Two-Dimensional Sources and Sinks
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Velocity Potentials and Stream
Richard Fitzpatrick
2016-03-31
![]() . Thus, it
follows from Equation (5.10) that uniform flow is irrotational. Hence, according to
Section 4.15, such flow can also be derived from a velocity potential. In fact, it is easily
demonstrated that
. Thus, it
follows from Equation (5.10) that uniform flow is irrotational. Hence, according to
Section 4.15, such flow can also be derived from a velocity potential. In fact, it is easily
demonstrated that