


Next: Kelvin Circulation Theorem
Up: Incompressible Inviscid Flow
Previous: Vortex Lines, Vortex Tubes,
Circulation and Vorticity
Consider a closed curve  situated entirely within a moving fluid. The
vector line integral (see Section A.14)
situated entirely within a moving fluid. The
vector line integral (see Section A.14)
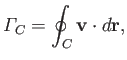 |
(4.76) |
where 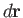 is an element of
is an element of  , and the integral is taken around the whole curve, is termed the circulation of the flow around the curve.
The sense of circulation (i.e., either clockwise or counter-clockwise) is arbitrary.
, and the integral is taken around the whole curve, is termed the circulation of the flow around the curve.
The sense of circulation (i.e., either clockwise or counter-clockwise) is arbitrary.
Let  be a surface having the closed curve
be a surface having the closed curve  for a boundary, and let
for a boundary, and let 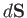 be an element of this surface (see Section A.7) with that direction of the normal which is related to the chosen sense of circulation around
be an element of this surface (see Section A.7) with that direction of the normal which is related to the chosen sense of circulation around  by the right-hand
circulation rule. (See Section A.8.) According to the curl theorem (see Section A.22),
by the right-hand
circulation rule. (See Section A.8.) According to the curl theorem (see Section A.22),
Thus, we conclude that circulation and vorticity are intimately related to one another. In fact, according to the
previous expression, the circulation of the fluid around loop  is equal to the net sum of the intensities of the
vortex filaments passing through the loop and piercing the surface
is equal to the net sum of the intensities of the
vortex filaments passing through the loop and piercing the surface  (with a filament making a
positive, or negative, contribution to the sum depending on whether it pierces the surface
in the direction determined by the chosen sense of circulation around
(with a filament making a
positive, or negative, contribution to the sum depending on whether it pierces the surface
in the direction determined by the chosen sense of circulation around  and the right-hand circulation rule, or in the opposite direction).
One important proviso to Equation (4.77) is that the surface
and the right-hand circulation rule, or in the opposite direction).
One important proviso to Equation (4.77) is that the surface  must lie entirely within the fluid.
must lie entirely within the fluid.



Next: Kelvin Circulation Theorem
Up: Incompressible Inviscid Flow
Previous: Vortex Lines, Vortex Tubes,
Richard Fitzpatrick
2016-03-31
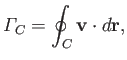
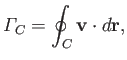
![]() be a surface having the closed curve
be a surface having the closed curve ![]() for a boundary, and let
for a boundary, and let ![]() be an element of this surface (see Section A.7) with that direction of the normal which is related to the chosen sense of circulation around
be an element of this surface (see Section A.7) with that direction of the normal which is related to the chosen sense of circulation around ![]() by the right-hand
circulation rule. (See Section A.8.) According to the curl theorem (see Section A.22),
by the right-hand
circulation rule. (See Section A.8.) According to the curl theorem (see Section A.22),