


Next: Rotation
Up: Vectors and Vector Fields
Previous: Vector Area
Vector Product
We have discovered how to construct a scalar from the components of two
general vectors, 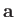 and
and 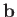 . Can we also construct a vector that is not
just a linear combination of
. Can we also construct a vector that is not
just a linear combination of 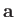 and
and 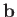 ? Consider the following definition:
? Consider the following definition:
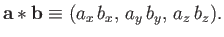 |
(A.36) |
Is
 a proper vector? Suppose that
a proper vector? Suppose that
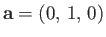 ,
,
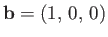 . In this case,
. In this case,
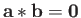 .
However, if we rotate the coordinate axes through
.
However, if we rotate the coordinate axes through  about
about 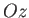 then
then
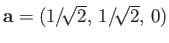 ,
,
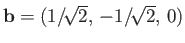 ,
and
,
and
 . Thus,
. Thus,
 does
not transform like a vector, because its magnitude depends on the choice of axes.
So, previous definition is a bad one.
does
not transform like a vector, because its magnitude depends on the choice of axes.
So, previous definition is a bad one.
Consider, now, the cross product or vector product:
 |
(A.37) |
Does this rather unlikely combination transform like a vector? Let us try
rotating the coordinate axes through an angle  about
about 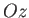 using Equations (A.20)-(A.22).
In the new coordinate system,
using Equations (A.20)-(A.22).
In the new coordinate system,
Thus, the  -component of
-component of
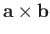 transforms correctly. It can
easily be shown that the other components transform correctly as well, and that
all components also transform correctly under rotation about
transforms correctly. It can
easily be shown that the other components transform correctly as well, and that
all components also transform correctly under rotation about  and
and  .
Thus,
.
Thus,
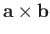 is a proper vector. Incidentally,
is a proper vector. Incidentally,
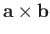 is the only simple combination of the components of two vectors that transforms
like a vector (which is non-coplanar with
is the only simple combination of the components of two vectors that transforms
like a vector (which is non-coplanar with  and
and  ).
The cross product is
anti-commutative,
).
The cross product is
anti-commutative,
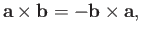 |
(A.39) |
distributive,
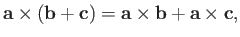 |
(A.40) |
but is not associative,
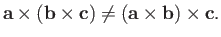 |
(A.41) |
The cross product transforms like a vector, which
means that it must have a well-defined direction and magnitude. We can show
that
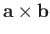 is perpendicular to both
is perpendicular to both  and
and  .
Consider
.
Consider
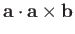 . If this is zero then the cross product
must be perpendicular to
. If this is zero then the cross product
must be perpendicular to  . Now,
. Now,
Therefore,
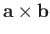 is perpendicular to
is perpendicular to  . Likewise, it can
be demonstrated that
. Likewise, it can
be demonstrated that
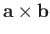 is perpendicular to
is perpendicular to  .
The vectors
.
The vectors 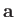 ,
, 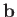 , and
, and
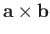 form a right-handed
set, like the unit vectors
form a right-handed
set, like the unit vectors 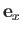 ,
, 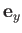 , and
, and  . In fact,
. In fact,
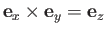 . This defines a unique direction for
. This defines a unique direction for
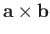 , which
is obtained from a right-hand rule. (See Figure A.8.)
, which
is obtained from a right-hand rule. (See Figure A.8.)
Figure:
The right-hand rule for cross products. Here,  is less that
is less that 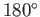 .
.
 |
Let us now evaluate the magnitude of
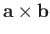 . We have
. We have
Thus,
 |
(A.44) |
where  is the angle subtended between
is the angle subtended between  and
and  .
Clearly,
.
Clearly,
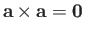 for any vector, because
for any vector, because  is always
zero in this case. Also, if
is always
zero in this case. Also, if
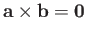 then either
then either
 ,
,
 , or
, or  is parallel (or antiparallel) to
is parallel (or antiparallel) to  .
.
Consider the parallelogram defined by the vectors  and
and  . (See Figure A.9.)
The scalar area of the parallelogram is
. (See Figure A.9.)
The scalar area of the parallelogram is
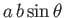 . By convention, the vector area has the magnitude of the
scalar area, and is normal to the plane of the parallelogram, in the sense obtained from a right-hand circulation rule by rotating
. By convention, the vector area has the magnitude of the
scalar area, and is normal to the plane of the parallelogram, in the sense obtained from a right-hand circulation rule by rotating  on to
on to
 (through an acute angle). In other words, if the fingers of the right-hand circulate in the direction of
rotation then the thumb of the right-hand indicates the direction of the vector area. So, the vector area is coming out of the
page in Figure A.9.
It follows that
(through an acute angle). In other words, if the fingers of the right-hand circulate in the direction of
rotation then the thumb of the right-hand indicates the direction of the vector area. So, the vector area is coming out of the
page in Figure A.9.
It follows that
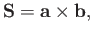 |
(A.45) |
Figure A.9:
A vector parallelogram.
 |
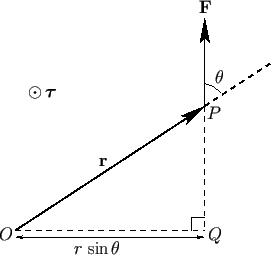
Suppose that a force 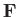 is applied at position
is applied at position  , as illustrated in Figure A.10.
The torque about the origin
, as illustrated in Figure A.10.
The torque about the origin 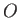 is the product of the magnitude of the force and
the length of the lever arm
is the product of the magnitude of the force and
the length of the lever arm 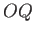 . Thus, the magnitude of the torque is
. Thus, the magnitude of the torque is
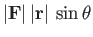 . The direction of the torque is conventionally defined as the direction of
the axis through
. The direction of the torque is conventionally defined as the direction of
the axis through 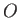 about which the force tries to rotate objects, in the sense
determined by a right-hand circulation rule. Hence, the torque is out of the page in Figure A.10.
It follows that the vector torque is
given by
about which the force tries to rotate objects, in the sense
determined by a right-hand circulation rule. Hence, the torque is out of the page in Figure A.10.
It follows that the vector torque is
given by
 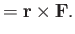 |
(A.46) |
Figure A.10:
A torque.
 |
The angular momentum, 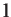 , of a particle of linear momentum
, of a particle of linear momentum 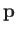 and position vector
and position vector  is simply defined as the moment of its
momentum about the origin: that is,
is simply defined as the moment of its
momentum about the origin: that is,
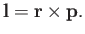 |
(A.47) |



Next: Rotation
Up: Vectors and Vector Fields
Previous: Vector Area
Richard Fitzpatrick
2016-03-31
![]() is perpendicular to both
is perpendicular to both ![]() and
and ![]() .
Consider
.
Consider
![]() . If this is zero then the cross product
must be perpendicular to
. If this is zero then the cross product
must be perpendicular to ![]() . Now,
. Now,
![]() . We have
. We have
![]() and
and ![]() . (See Figure A.9.)
The scalar area of the parallelogram is
. (See Figure A.9.)
The scalar area of the parallelogram is
![]() . By convention, the vector area has the magnitude of the
scalar area, and is normal to the plane of the parallelogram, in the sense obtained from a right-hand circulation rule by rotating
. By convention, the vector area has the magnitude of the
scalar area, and is normal to the plane of the parallelogram, in the sense obtained from a right-hand circulation rule by rotating ![]() on to
on to
![]() (through an acute angle). In other words, if the fingers of the right-hand circulate in the direction of
rotation then the thumb of the right-hand indicates the direction of the vector area. So, the vector area is coming out of the
page in Figure A.9.
It follows that
(through an acute angle). In other words, if the fingers of the right-hand circulate in the direction of
rotation then the thumb of the right-hand indicates the direction of the vector area. So, the vector area is coming out of the
page in Figure A.9.
It follows that
![]() is applied at position
is applied at position ![]() , as illustrated in Figure A.10.
The torque about the origin
, as illustrated in Figure A.10.
The torque about the origin ![]() is the product of the magnitude of the force and
the length of the lever arm
is the product of the magnitude of the force and
the length of the lever arm ![]() . Thus, the magnitude of the torque is
. Thus, the magnitude of the torque is
![]() . The direction of the torque is conventionally defined as the direction of
the axis through
. The direction of the torque is conventionally defined as the direction of
the axis through ![]() about which the force tries to rotate objects, in the sense
determined by a right-hand circulation rule. Hence, the torque is out of the page in Figure A.10.
It follows that the vector torque is
given by
about which the force tries to rotate objects, in the sense
determined by a right-hand circulation rule. Hence, the torque is out of the page in Figure A.10.
It follows that the vector torque is
given by
![]() , of a particle of linear momentum
, of a particle of linear momentum ![]() and position vector
and position vector ![]() is simply defined as the moment of its
momentum about the origin: that is,
is simply defined as the moment of its
momentum about the origin: that is,