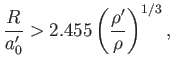Next: Exercises
Up: Hydrostatics
Previous: Jacobi Ellipsoids
Consider a homogeneous liquid moon of mass 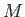 that is in a circular orbit of radius
that is in a circular orbit of radius 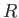 about a planet of mass
about a planet of mass  . Let
. Let
 ,
,  , and
, and 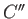 be the center of the moon, the center of the planet, and the center of mass of the moon-planet
system, respectively. As is easily demonstrated, all three points lie on the same straight-line, and the distances between them
take the constant values
be the center of the moon, the center of the planet, and the center of mass of the moon-planet
system, respectively. As is easily demonstrated, all three points lie on the same straight-line, and the distances between them
take the constant values 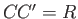 and
and
![$ CC'' = [M'/(M+M')]\,R$](img971.png) (Fitzpatrick 2012).
Moreover, according to standard Newtonian dynamics, there exists an inertial frame of reference in which
(Fitzpatrick 2012).
Moreover, according to standard Newtonian dynamics, there exists an inertial frame of reference in which 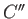 is stationary, and the line
is stationary, and the line 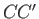 rotates
at the fixed angular velocity
rotates
at the fixed angular velocity
 , where (Fitzpatrick 2012)
, where (Fitzpatrick 2012)
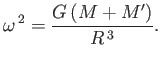 |
(2.146) |
In other words, in the inertial frame, the moon and the planet orbit in a fixed plane about their common center of mass at the angular velocity  .
It is convenient to transform to a non-inertial reference frame that
rotates (with respect to the inertial frame), about an axis passing through
.
It is convenient to transform to a non-inertial reference frame that
rotates (with respect to the inertial frame), about an axis passing through 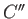 , at the angular velocity
, at the angular velocity
 . It follows
that points
. It follows
that points  ,
,  , and
, and 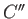 appear stationary in this frame. It is also convenient to adopt
the standard right-handed Cartesian coordinates,
appear stationary in this frame. It is also convenient to adopt
the standard right-handed Cartesian coordinates, 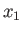 ,
, 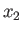 ,
, 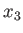 , and to choose the coordinate axes
such that
, and to choose the coordinate axes
such that

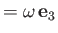 ,
,
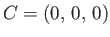 ,
,
 , and
, and
![$ C''=([M'/(M+M')]\,R,\,0,\,0)$](img977.png) .
Thus, in the non-inertial reference frame, the orbital rotation axis runs parallel to the
.
Thus, in the non-inertial reference frame, the orbital rotation axis runs parallel to the 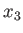 -axis, and the centers of the moon and the planet both lie on the
-axis, and the centers of the moon and the planet both lie on the 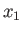 -axis.
-axis.
Suppose that the moon does not rotate (about an axis passing through its center of mass) in the non-inertial reference frame. This implies that, in the inertial
frame, the moon appears to rotate about an axis parallel to the 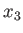 -axis, and passing through
-axis, and passing through  , at the same angular velocity as
it orbits about
, at the same angular velocity as
it orbits about 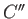 . This type of rotation is termed synchronous, and ensures that the same
hemisphere of the moon is always directed toward the planet. Such rotation is fairly common in the solar system. For instance,
the Moon rotates synchronously in such a manner that the same hemisphere is always visible from the Earth. Synchronous
rotation in the solar system is a consequence of process known as tidal locking (Murray and Dermott 1999).
. This type of rotation is termed synchronous, and ensures that the same
hemisphere of the moon is always directed toward the planet. Such rotation is fairly common in the solar system. For instance,
the Moon rotates synchronously in such a manner that the same hemisphere is always visible from the Earth. Synchronous
rotation in the solar system is a consequence of process known as tidal locking (Murray and Dermott 1999).
Because a synchronously rotating moon is completely stationary in the aforementioned non-inertial frame, its internal pressure,  , is governed by a force balance
equation of the form [cf., Equation (2.83)]
, is governed by a force balance
equation of the form [cf., Equation (2.83)]
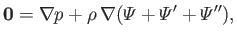 |
(2.147) |
where  is the uniform internal mass density,
is the uniform internal mass density,
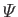 the gravitational potential due to the moon,
the gravitational potential due to the moon,
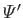 the gravitational potential due to the planet, and
the gravitational potential due to the planet, and
![$\displaystyle {\mit\Psi}'' = -\frac{1}{2}\,\omega^2\left[\left(x_1-\frac{M'}{M+M'}\,R\right)^2+x_2^{\,2}\right]$](img980.png) |
(2.148) |
the centrifugal potential due to the fact that the non-inertial frame is rotating (about an axis parallel to the 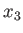 -axis
and passing through point
-axis
and passing through point 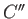 ) at the angular velocity
) at the angular velocity  [cf., Equation (2.84)]. Suppose that the moon is much less massive that the planet
(i.e.,
[cf., Equation (2.84)]. Suppose that the moon is much less massive that the planet
(i.e., 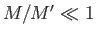 ). In this limit, the centrifugal potential (2.148) reduces to
). In this limit, the centrifugal potential (2.148) reduces to
![$\displaystyle {\mit\Psi}'' \simeq -\left[\frac{1}{2}-\frac{x_1}{R}+\frac{(1/2)\,x_1^{\,2}+(1/2)\,x_2^{\,2}}{R^{\,2}}\right],$](img982.png) |
(2.149) |
where use has been made of Equation (2.146).
Suppose that the planet is spherical. It follows that the potential
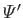 is the same as that which would
be generated by a point mass
is the same as that which would
be generated by a point mass  located at
located at  . In other words,
. In other words,
where we have expanded up to second order in 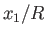 , et cetera.
, et cetera.
The previous two equations can be combined to give
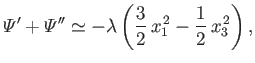 |
(2.151) |
where
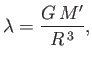 |
(2.152) |
and any
constant terms have been neglected. Thus, the net force field experienced by the moon due to the combined action of the fictitious centrifugal
force and the gravitational force field of the planet is
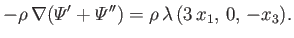 |
(2.153) |
The previous type of force field is known as a tidal force field, and clearly acts to elongate the moon along the axis joining the
centers of the moon and planet (i.e., the 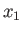 -axis), and to compress it along the orbital rotation axis (i.e., the
-axis), and to compress it along the orbital rotation axis (i.e., the
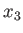 -axis). Moreover, the magnitude of the
tidal force increases linearly with distance from the center of the moon. The tidal force field is a consequence of the different spatial
variation of the centrifugal force and the planet's gravitational force of attraction. This different variation causes these two forces, which
balance one another at the center of the moon, to not balance away from the center (Fitzpatrick 2012).
As a result of the tidal force
field, we expect the shape of the moon to be distorted from a sphere. Of course, the moon also generates a tidal
force field that acts to distort the shape of the planet. However, we are assuming that the tidal distortion of the
planet is much smaller than that of the moon (which justifies our earlier statement that the planet is essentially
spherical). As will be demonstrated later, this assumption is reasonable provided the mass of the moon is
much less than that of the planet (assuming that the planet and moon have similar densities).
-axis). Moreover, the magnitude of the
tidal force increases linearly with distance from the center of the moon. The tidal force field is a consequence of the different spatial
variation of the centrifugal force and the planet's gravitational force of attraction. This different variation causes these two forces, which
balance one another at the center of the moon, to not balance away from the center (Fitzpatrick 2012).
As a result of the tidal force
field, we expect the shape of the moon to be distorted from a sphere. Of course, the moon also generates a tidal
force field that acts to distort the shape of the planet. However, we are assuming that the tidal distortion of the
planet is much smaller than that of the moon (which justifies our earlier statement that the planet is essentially
spherical). As will be demonstrated later, this assumption is reasonable provided the mass of the moon is
much less than that of the planet (assuming that the planet and moon have similar densities).
Suppose that the bounding surface of the moon is the ellipsoid
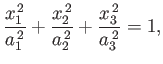 |
(2.154) |
where
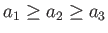 . It follows, from Appendix D, that the gravitational potential
of the moon at an interior point can be written
. It follows, from Appendix D, that the gravitational potential
of the moon at an interior point can be written
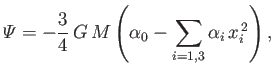 |
(2.155) |
where the integrals 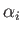 , for
, for 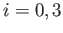 , are defined in Equations (D.30) and (D.31).
Hence, from Equations (2.147) and (2.151), the pressure distribution within the moon is given by
, are defined in Equations (D.30) and (D.31).
Hence, from Equations (2.147) and (2.151), the pressure distribution within the moon is given by
![$\displaystyle p = p_0 -\frac{1}{2}\,\rho\left[\left(\frac{3}{2}\,G\,M\,\alpha_1...
..._2\,x_2^{\,2}+\left(\frac{3}{2}\,G\,M\,\alpha_3+\lambda\right)x_3^{\,2}\right],$](img992.png) |
(2.156) |
where 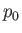 is the central pressure. The pressure must be zero on the moon's bounding surface, otherwise this surface
would not be in equilibrium.
Thus, in order to achieve equilibrium, we require
is the central pressure. The pressure must be zero on the moon's bounding surface, otherwise this surface
would not be in equilibrium.
Thus, in order to achieve equilibrium, we require
![$\displaystyle \frac{1}{2}\,\rho\left[\left(\frac{3}{2}\,G\,M\,\alpha_1-3\,\lamb...
...2^{\,2}+\left(\frac{3}{2}\,G\,M\,\alpha_3+\lambda\right)x_3^{\,2}\right] = p_0,$](img993.png) |
(2.157) |
whenever
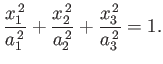 |
(2.158) |
The previous two equations can only be simultaneously satisfied if
![$\displaystyle \left[\alpha_1-\frac{3\,\lambda}{(3/2)\,G\,M}\right]a_1^{\,2} =\alpha_2\,a_2^{\,2} = \left[\alpha_3+\frac{\lambda}{(3/2)\,G\,M}\right] a_3^{\,2}.$](img994.png) |
(2.159) |
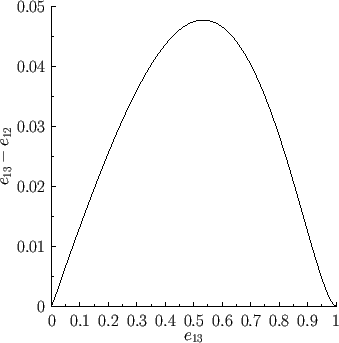
Figure 2.8:
Properties of the Roche ellipsoids.
 |
Let
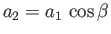 and
and
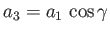 , where
, where
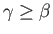 . It is also helpful
to define
. It is also helpful
to define
 . With the help of some of the analysis
presented in the previous section, the integrals
. With the help of some of the analysis
presented in the previous section, the integrals 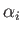 , for
, for 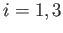 , can be shown to take the form
, can be shown to take the form
where the incomplete elliptic integrals
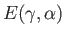 and
and
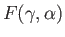 are defined in Equations (2.141)
and (2.142), respectively. Thus, Equation (2.159) yields
are defined in Equations (2.141)
and (2.142), respectively. Thus, Equation (2.159) yields
subject to the constraint
where
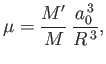 |
(2.165) |
and
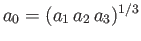 is the mean radius of the moon. The dimensionless parameter
is the mean radius of the moon. The dimensionless parameter 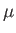 measures the strength of the tidal distortion field, generated by the planet, that acts on the moon. There
is an analogous parameter,
measures the strength of the tidal distortion field, generated by the planet, that acts on the moon. There
is an analogous parameter,
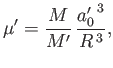 |
(2.166) |
where 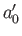 is the mean radius of the planet, which measures the tidal distortion field, generated by the
moon, that acts on the planet. We previously assumed that the former distortion field is much
stronger than the latter, allowing us to neglect the tidal distortion of the planet altogether, and so to treat it
as a sphere. This assumption is only justified if
is the mean radius of the planet, which measures the tidal distortion field, generated by the
moon, that acts on the planet. We previously assumed that the former distortion field is much
stronger than the latter, allowing us to neglect the tidal distortion of the planet altogether, and so to treat it
as a sphere. This assumption is only justified if
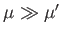 , which implies that
, which implies that
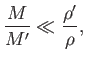 |
(2.167) |
where
![$ \rho=M/[(4/3)\,\pi\,a_0^{\,3}]$](img1019.png) and
and
![$ \rho'=M'/[(4/3)\,\pi\,{a_0'}^{\,3}]$](img1020.png) are the mean densities of the
moon and the planet, respectively. Assuming that these densities are similar, the previous condition reduces to
are the mean densities of the
moon and the planet, respectively. Assuming that these densities are similar, the previous condition reduces to
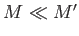 , or, equivalently,
, or, equivalently, 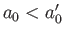 . In other words, neglecting the tidal distortion of the planet, while retaining that of the moon,
is generally only reasonable when the mass of the moon is much less than that of the planet, as was previously assumed
to be the case.
. In other words, neglecting the tidal distortion of the planet, while retaining that of the moon,
is generally only reasonable when the mass of the moon is much less than that of the planet, as was previously assumed
to be the case.
Table 2.3:
Properties of the Roche ellipsoids.
| |
|
|
|
|
|
|
|
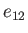
|
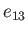
|
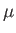
|
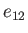
|
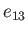
|
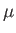
|
|
|
| |
|
|
|
|
|
|
|
| 0.00 |
0.00000 |
0.00000 |
0.52 |
0.56740 |
0.33440 |
|
|
| 0.04 |
0.04613 |
0.00213 |
0.56 |
0.60632 |
0.38204 |
|
|
| 0.08 |
0.09223 |
0.00852 |
0.60 |
0.64445 |
0.43094 |
|
|
| 0.12 |
0.13809 |
0.01913 |
0.64 |
0.68182 |
0.48027 |
|
|
| 0.16 |
0.18364 |
0.03392 |
0.68 |
0.71848 |
0.52890 |
|
|
| 0.20 |
0.22879 |
0.05282 |
0.72 |
0.75446 |
0.57532 |
|
|
| 0.24 |
0.27346 |
0.07573 |
0.76 |
0.78984 |
0.61729 |
|
|
| 0.28 |
0.31756 |
0.10253 |
0.80 |
0.82472 |
0.65150 |
|
|
| 0.32 |
0.36104 |
0.13308 |
0.84 |
0.85923 |
0.67265 |
|
|
| 0.36 |
0.40383 |
0.16721 |
0.88 |
0.89353 |
0.67151 |
|
|
| 0.40 |
0.44588 |
0.20470 |
0.92 |
0.92793 |
0.62978 |
|
|
| 0.44 |
0.48718 |
0.24528 |
0.96 |
0.96294 |
0.50135 |
|
|
| 0.48 |
0.52769 |
0.28865 |
1.00 |
1.00000 |
0.00000 |
|
|
|
Equations (2.163) and (2.164), which describe the ellipsoidal equilibria of
a synchronously rotating, relatively low mass, liquid moon due to the tidal force field of the planet about which it orbits,
were first obtained by Édouard Roche (1820-1883) in 1850. The properties of the so-called Roche ellipsoids are
set out in Table 2.3, and Figures 2.8 and 2.9.
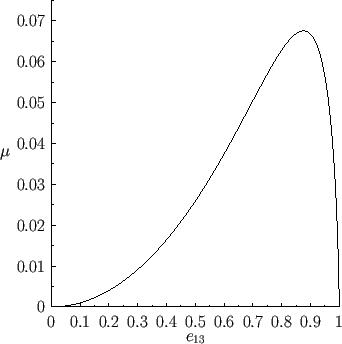
Figure 2.9:
Properties of the Roche ellipsoids.
 |
It can be seen, from Table 2.3 and Figure 2.8, that the eccentricity
 of a Roche ellipsoid in the
of a Roche ellipsoid in the 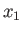 -
-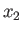 plane is almost equal to its eccentricity
plane is almost equal to its eccentricity
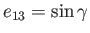 in the
in the 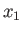 -
-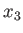 plane. In other words,
Roche ellipsoids are almost spheroidal in shape, being elongated along the
plane. In other words,
Roche ellipsoids are almost spheroidal in shape, being elongated along the 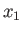 -axis (i.e., the axis
joining the centers of the moon and the planet), and compressed by almost equal amounts along the
-axis (i.e., the axis
joining the centers of the moon and the planet), and compressed by almost equal amounts along the 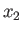 - and
- and 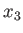 -axes.
In the limit
-axes.
In the limit 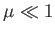 , in which the tidal distortion field due to the planet is weak, it
is easily shown that
, in which the tidal distortion field due to the planet is weak, it
is easily shown that
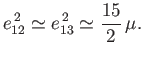 |
(2.168) |
For the case of the tidal distortion field generated by the Earth, and acting on the Moon, which is characterized by
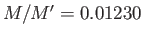 and
and
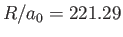 ,
we obtain
,
we obtain
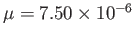 (Yoder 1995). It follows that
(Yoder 1995). It follows that
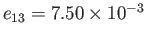 , and
, and
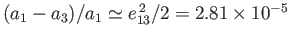 . In other words, were the Moon a homogeneous
liquid body, the elongation generated by the tidal field of the Earth would be about
. In other words, were the Moon a homogeneous
liquid body, the elongation generated by the tidal field of the Earth would be about
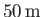 .
.
It can be seen, from Table 2.3 and Figure 2.9, that the parameter 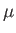 attains a maximum value as the
eccentricity of a Roche ellipsoid varies from 0 to 1. In fact, this maximum value,
attains a maximum value as the
eccentricity of a Roche ellipsoid varies from 0 to 1. In fact, this maximum value,
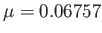 , occurs when
, occurs when
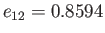 and
and
 . It follows that there is a maximum strength of the tidal distortion field, generated by a planet,
that is consistent with an ellipsoidal equilibrium of a synchronously rotating, homogeneous, liquid moon in a circular orbit about the planet. It is plausible that if this maximum strength is
exceeded then the moon is tidally disrupted by the planet. The equilibrium condition
. It follows that there is a maximum strength of the tidal distortion field, generated by a planet,
that is consistent with an ellipsoidal equilibrium of a synchronously rotating, homogeneous, liquid moon in a circular orbit about the planet. It is plausible that if this maximum strength is
exceeded then the moon is tidally disrupted by the planet. The equilibrium condition
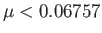 is
equivalent to
is
equivalent to
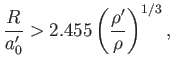 |
(2.169) |
where
![$ \rho=M/[(4/3)\,\pi\,a_0^{\,3}]$](img1019.png) and
and
![$ \rho'=M'/[(4/3)\,\pi\,{a_0'}^{\,3}]$](img1020.png) are the mean densities of the moon
and the planet, respectively. According to the previous expression, there is a minimum orbital radius of a moon circling
a planet. Below this radius, which is called the Roche radius, the moon is presumably torn apart by tidal effects.
The Roche radius for a synchronously rotating, self-gravitating, liquid moon in a circular orbit about a spherical planet is about
are the mean densities of the moon
and the planet, respectively. According to the previous expression, there is a minimum orbital radius of a moon circling
a planet. Below this radius, which is called the Roche radius, the moon is presumably torn apart by tidal effects.
The Roche radius for a synchronously rotating, self-gravitating, liquid moon in a circular orbit about a spherical planet is about 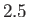 times the planet's radius (assuming that the moon and the planet have approximately the same mass density). Of course, relatively small objects, such as
artificial satellites, which are held together by internal tensile strength, rather than gravity, can orbit inside the Roche radius without
being disrupted.
times the planet's radius (assuming that the moon and the planet have approximately the same mass density). Of course, relatively small objects, such as
artificial satellites, which are held together by internal tensile strength, rather than gravity, can orbit inside the Roche radius without
being disrupted.



Next: Exercises
Up: Hydrostatics
Previous: Jacobi Ellipsoids
Richard Fitzpatrick
2016-03-31
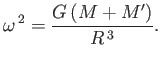
![]() -axis, and passing through
-axis, and passing through ![]() , at the same angular velocity as
it orbits about
, at the same angular velocity as
it orbits about ![]() . This type of rotation is termed synchronous, and ensures that the same
hemisphere of the moon is always directed toward the planet. Such rotation is fairly common in the solar system. For instance,
the Moon rotates synchronously in such a manner that the same hemisphere is always visible from the Earth. Synchronous
rotation in the solar system is a consequence of process known as tidal locking (Murray and Dermott 1999).
. This type of rotation is termed synchronous, and ensures that the same
hemisphere of the moon is always directed toward the planet. Such rotation is fairly common in the solar system. For instance,
the Moon rotates synchronously in such a manner that the same hemisphere is always visible from the Earth. Synchronous
rotation in the solar system is a consequence of process known as tidal locking (Murray and Dermott 1999).
![]() , is governed by a force balance
equation of the form [cf., Equation (2.83)]
, is governed by a force balance
equation of the form [cf., Equation (2.83)]
![]() is the same as that which would
be generated by a point mass
is the same as that which would
be generated by a point mass ![]() located at
located at ![]() . In other words,
. In other words,
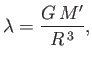
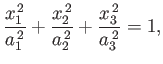
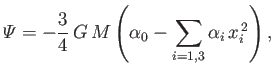
![$\displaystyle p = p_0 -\frac{1}{2}\,\rho\left[\left(\frac{3}{2}\,G\,M\,\alpha_1...
..._2\,x_2^{\,2}+\left(\frac{3}{2}\,G\,M\,\alpha_3+\lambda\right)x_3^{\,2}\right],$](img992.png)
![$\displaystyle \frac{1}{2}\,\rho\left[\left(\frac{3}{2}\,G\,M\,\alpha_1-3\,\lamb...
...2^{\,2}+\left(\frac{3}{2}\,G\,M\,\alpha_3+\lambda\right)x_3^{\,2}\right] = p_0,$](img993.png)
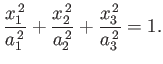
![]() and
and
![]() , where
, where
![]() . It is also helpful
to define
. It is also helpful
to define
![]() . With the help of some of the analysis
presented in the previous section, the integrals
. With the help of some of the analysis
presented in the previous section, the integrals ![]() , for
, for ![]() , can be shown to take the form
, can be shown to take the form

![$\displaystyle =\frac{2}{a_1^{\,2}\,\sin^3\gamma}\left[\frac{E(\gamma,\alpha)}{\...
...{\sin^2\alpha} - \frac{\cos\gamma\,\sin\gamma}{\cos^2\alpha\,\cos\beta}\right],$](img1003.png)
![$\displaystyle = \frac{2}{a_1^{\,2}\,\sin^3\gamma}\left[-\frac{E(\gamma,\alpha)}{\cos^2\alpha} + \frac{\cos\beta\,\sin\gamma}{\cos^2\alpha\,\cos\gamma}\right],$](img1005.png)
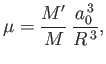
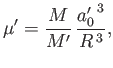
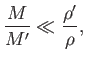
![]() of a Roche ellipsoid in the
of a Roche ellipsoid in the ![]() -
-![]() plane is almost equal to its eccentricity
plane is almost equal to its eccentricity
![]() in the
in the ![]() -
-![]() plane. In other words,
Roche ellipsoids are almost spheroidal in shape, being elongated along the
plane. In other words,
Roche ellipsoids are almost spheroidal in shape, being elongated along the ![]() -axis (i.e., the axis
joining the centers of the moon and the planet), and compressed by almost equal amounts along the
-axis (i.e., the axis
joining the centers of the moon and the planet), and compressed by almost equal amounts along the ![]() - and
- and ![]() -axes.
In the limit
-axes.
In the limit ![]() , in which the tidal distortion field due to the planet is weak, it
is easily shown that
, in which the tidal distortion field due to the planet is weak, it
is easily shown that
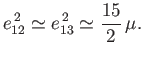
![]() attains a maximum value as the
eccentricity of a Roche ellipsoid varies from 0 to 1. In fact, this maximum value,
attains a maximum value as the
eccentricity of a Roche ellipsoid varies from 0 to 1. In fact, this maximum value,
![]() , occurs when
, occurs when
![]() and
and
![]() . It follows that there is a maximum strength of the tidal distortion field, generated by a planet,
that is consistent with an ellipsoidal equilibrium of a synchronously rotating, homogeneous, liquid moon in a circular orbit about the planet. It is plausible that if this maximum strength is
exceeded then the moon is tidally disrupted by the planet. The equilibrium condition
. It follows that there is a maximum strength of the tidal distortion field, generated by a planet,
that is consistent with an ellipsoidal equilibrium of a synchronously rotating, homogeneous, liquid moon in a circular orbit about the planet. It is plausible that if this maximum strength is
exceeded then the moon is tidally disrupted by the planet. The equilibrium condition
![]() is
equivalent to
is
equivalent to