


Next: Cylindrical Airfoils
Up: Incompressible Aerodynamics
Previous: Introduction
Consider a two-dimensional airfoil that is at rest in a uniform wind of speed  whose direction subtends a (clockwise) angle
whose direction subtends a (clockwise) angle  with the negative
with the negative  -axis. It follows that the wind velocity is
-axis. It follows that the wind velocity is
 , and the
corresponding complex velocity is
, and the
corresponding complex velocity is
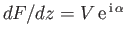 . (See Section 6.4.)
The air velocity a great distance from the airfoil must tend toward this uniform velocity.
Thus, for sufficiently large
. (See Section 6.4.)
The air velocity a great distance from the airfoil must tend toward this uniform velocity.
Thus, for sufficiently large  , we can write (see Section 6.4)
, we can write (see Section 6.4)
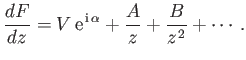 |
(9.3) |
According to Equation (6.172), the circulation,
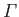 , of air about the airfoil is determined by
performing the integral
, of air about the airfoil is determined by
performing the integral
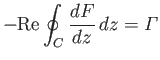 |
(9.4) |
around a loop  that lies just above the airfoil surface.
However, as discussed in Section 6.10, the value of this integral is unchanged if it is performed around any loop that can be continuously deformed onto
that lies just above the airfoil surface.
However, as discussed in Section 6.10, the value of this integral is unchanged if it is performed around any loop that can be continuously deformed onto  , while
not passing through the airfoil surface, or crossing a singularity of the complex velocity,
, while
not passing through the airfoil surface, or crossing a singularity of the complex velocity, 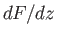 (i.e., a line source or a
(i.e., a line source or a  -directed vortex
filament).
Because (in the high Reynolds number limit in which the boundary layer and the wake are infinitely thin) there are no line sources or
-directed vortex
filament).
Because (in the high Reynolds number limit in which the boundary layer and the wake are infinitely thin) there are no line sources or  -directed vortex filaments external to the airfoil, we can evaluate the integral around a large circle of radius
-directed vortex filaments external to the airfoil, we can evaluate the integral around a large circle of radius 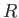 , centered on the origin. It follows that
, centered on the origin. It follows that
 and
and
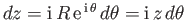 . Hence,
. Hence,
![$\displaystyle {\mit\Gamma}= -{\rm Re}\left({\rm i}\oint\left[V\,R\,{\rm e}^{\,{...
...eta+\alpha)} + A + {\cal O}(R^{\,-1})\right]d\theta\right) = 2\pi\,{\rm Im}(A),$](img3281.png) |
(9.5) |
which implies that
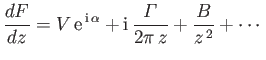 |
(9.6) |
at large 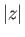 .
.
As discussed in Section 6.11, the net force (per unit length) acting on the airfoil,
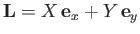 , is determined by performing the Blasius integral,
, is determined by performing the Blasius integral,
 |
(9.7) |
around a loop  that lies just above the airfoil surface. However, as before, the value of the integral is unchanged
if instead we perform it around a large circle of radius
that lies just above the airfoil surface. However, as before, the value of the integral is unchanged
if instead we perform it around a large circle of radius  , centered on the origin.
Far from the airfoil,
, centered on the origin.
Far from the airfoil,
 |
(9.8) |
So, we
obtain
![$\displaystyle X -{\rm i}\,Y = \frac{1}{2}\,{\rm i^{\,2}}\,\rho\oint\left[V^{\,2...
...\right] d\theta = -{\rm i}\,{\rm e}^{\,{\rm i}\,\alpha}\,\rho\,V\,{\mit\Gamma},$](img3286.png) |
(9.9) |
or
 |
(9.10) |
In other words, the resultant force (per unit length) acting on the airfoil is of magnitude
 , and
has the direction obtained by rotating the wind vector through a right-angle in the sense opposite to that of the circulation.
This type of force is known as lift, and is responsible for flight. The result (9.10) is
known as the theorem of Kutta and Zhukovskii, after the German scientist M.W. Kutta (1867-1944), and the
Russian scientist N.E. Zhukovskii (1847-1921), who discovered it independently.
Note that (at fixed circulation) the lift is independent of the shape of the airfoil. Furthermore, according to the Kutta-Zhukovskii
theorem, there is zero drag acting on the airfoil (i.e., zero force acting in the direction of the wind). In reality,
there is always a small friction drag due to air viscosity, as well as a (hopefully) small form drag due to residual
separation of the boundary layer from the back of the airfoil. There is actually a third type of drag, known as induced drag, that is
discussed in Section 9.8.
, and
has the direction obtained by rotating the wind vector through a right-angle in the sense opposite to that of the circulation.
This type of force is known as lift, and is responsible for flight. The result (9.10) is
known as the theorem of Kutta and Zhukovskii, after the German scientist M.W. Kutta (1867-1944), and the
Russian scientist N.E. Zhukovskii (1847-1921), who discovered it independently.
Note that (at fixed circulation) the lift is independent of the shape of the airfoil. Furthermore, according to the Kutta-Zhukovskii
theorem, there is zero drag acting on the airfoil (i.e., zero force acting in the direction of the wind). In reality,
there is always a small friction drag due to air viscosity, as well as a (hopefully) small form drag due to residual
separation of the boundary layer from the back of the airfoil. There is actually a third type of drag, known as induced drag, that is
discussed in Section 9.8.
As discussed in Section 6.11, the net moment per unit length (about the origin),  , acting on the airfoil
is determined by performing the integral
, acting on the airfoil
is determined by performing the integral
![$\displaystyle {\rm Re}\left[-\frac{1}{2}\,\rho \oint_C \left(\frac{dF}{dz}\right)^{\,2} z\,dz\right]=M$](img3289.png) |
(9.11) |
around a loop  that lies just above the airfoil surface. As before, we can deform
that lies just above the airfoil surface. As before, we can deform  into a
circle of radius
into a
circle of radius 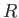 , centered on the origin, without changing the value of the integral.
Hence, we obtain
, centered on the origin, without changing the value of the integral.
Hence, we obtain
or
![$\displaystyle M = {\rm Re} \left[2\pi\,\rho\,V\,B\,{\rm e}^{\,{\rm i}\,(\alpha-\pi/2)}\right].$](img3292.png) |
(9.13) |



Next: Cylindrical Airfoils
Up: Incompressible Aerodynamics
Previous: Introduction
Richard Fitzpatrick
2016-03-31
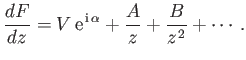
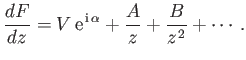
![]() , of air about the airfoil is determined by
performing the integral
, of air about the airfoil is determined by
performing the integral
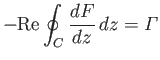
![$\displaystyle {\mit\Gamma}= -{\rm Re}\left({\rm i}\oint\left[V\,R\,{\rm e}^{\,{...
...eta+\alpha)} + A + {\cal O}(R^{\,-1})\right]d\theta\right) = 2\pi\,{\rm Im}(A),$](img3281.png)
![]() , is determined by performing the Blasius integral,
, is determined by performing the Blasius integral,
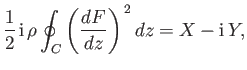

![$\displaystyle X -{\rm i}\,Y = \frac{1}{2}\,{\rm i^{\,2}}\,\rho\oint\left[V^{\,2...
...\right] d\theta = -{\rm i}\,{\rm e}^{\,{\rm i}\,\alpha}\,\rho\,V\,{\mit\Gamma},$](img3286.png)
![]() , acting on the airfoil
is determined by performing the integral
, acting on the airfoil
is determined by performing the integral
![$\displaystyle {\rm Re}\left[-\frac{1}{2}\,\rho \oint_C \left(\frac{dF}{dz}\right)^{\,2} z\,dz\right]=M$](img3289.png)
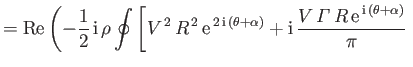
![$\displaystyle \phantom{=}\left.\left.+ \frac{8\pi^2\,V\,B\,{\rm e}^{\,{\rm i}\,\alpha}-{\mit\Gamma}^{\,2}}{4\pi^2}+{\cal O}(R^{\,-1})\right] d\theta\right) ,$](img3291.png)