


Next: Blasius Theorem
Up: Two-Dimensional Potential Flow
Previous: Free Streamline Theory
Complex Line Integrals
Consider the line integral of some function  of the complex variable taken (counter-clockwise) around a closed curve
of the complex variable taken (counter-clockwise) around a closed curve  in the complex
plane:
in the complex
plane:
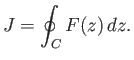 |
(6.158) |
Because
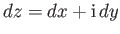 , and writing
, and writing
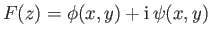 , where
, where 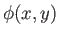 and
and 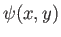 are real functions,
it follows that
are real functions,
it follows that
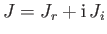 , where
, where
However, we can also write the previous expressions in the two-dimensional vector form
where
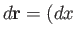 ,
, 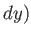 ,
,
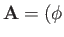 ,
, 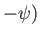 , and
, and
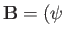 ,
, 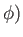 . According to
the curl theorem (see Section A.22),
. According to
the curl theorem (see Section A.22),
where  is the region of the
is the region of the  -
- plane enclosed by
plane enclosed by  . Hence, we obtain
. Hence, we obtain
Let
where  is a closed curve in the complex plane that completely surrounds the smaller curve
is a closed curve in the complex plane that completely surrounds the smaller curve  .
Consider
.
Consider
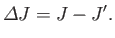 |
(6.169) |
Writing
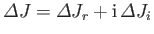 , a direct generalization of the previous analysis
reveals that
, a direct generalization of the previous analysis
reveals that
where  is now the region of the
is now the region of the  -
- plane lying between the curves
plane lying between the curves  and
and  .
Suppose that
.
Suppose that  is well-behaved (i.e., finite, single-valued, and
differentiable) throughout
is well-behaved (i.e., finite, single-valued, and
differentiable) throughout  . It immediately follows that its real and imaginary components,
. It immediately follows that its real and imaginary components, 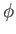 and
and  ,
respectively, satisfy the Cauchy-Riemann relations, (6.17)-(6.18), throughout
,
respectively, satisfy the Cauchy-Riemann relations, (6.17)-(6.18), throughout  .
However, if this is the case then it is apparent, from the previous two expressions, that
.
However, if this is the case then it is apparent, from the previous two expressions, that
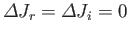 .
In other words, if
.
In other words, if  is well-behaved throughout
is well-behaved throughout  then
then  .
.
The circulation of the flow about some closed curve  in the
in the  -
- plane is defined
plane is defined
 |
(6.172) |
where  is the complex velocity potential of the flow, and use has been made of Equation (6.35). Thus, the circulation can be evaluated by performing a line integral in the complex
is the complex velocity potential of the flow, and use has been made of Equation (6.35). Thus, the circulation can be evaluated by performing a line integral in the complex  -plane. Moreover, as is clear from the previous discussion, this integral can be performed around any loop that can be continuously deformed into the loop
-plane. Moreover, as is clear from the previous discussion, this integral can be performed around any loop that can be continuously deformed into the loop  while
still remaining in the fluid, and not passing over a singularity of the complex velocity,
while
still remaining in the fluid, and not passing over a singularity of the complex velocity, 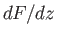 .
.



Next: Blasius Theorem
Up: Two-Dimensional Potential Flow
Previous: Free Streamline Theory
Richard Fitzpatrick
2016-03-31
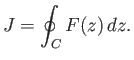
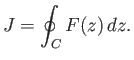
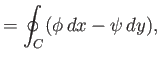
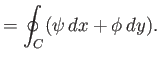
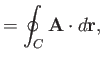
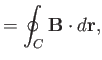
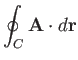

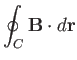
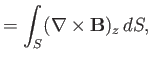
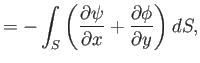
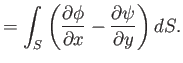
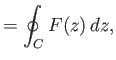
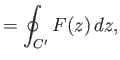

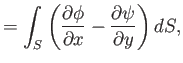
![]() in the
in the ![]() -
-![]() plane is defined
plane is defined