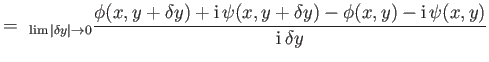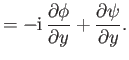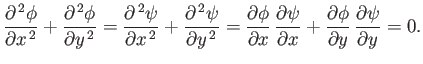Next: Complex Velocity Potential
Up: Two-Dimensional Potential Flow
Previous: Complex Functions
Cauchy-Riemann Relations
We can define the derivative of a complex function in the same way that we define the derivative of a real function. In other words,
 |
(6.13) |
However, we now have a problem. If  is a well-behaved
function (i.e., finite, single-valued, and differentiable) then it should not matter from which direction in the complex
plane we approach the point
is a well-behaved
function (i.e., finite, single-valued, and differentiable) then it should not matter from which direction in the complex
plane we approach the point  when taking the limit in Equation (6.13).
There are, of course, many
different possible approach directions, but if we look at a regular complex
function,
when taking the limit in Equation (6.13).
There are, of course, many
different possible approach directions, but if we look at a regular complex
function,
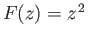 (say), then
(say), then
 |
(6.14) |
is perfectly well-defined, and is, therefore, completely independent of the details of
how the limit is taken in Equation (6.13).
The fact that Equation (6.13)
has to give the same result, no matter from which direction we approach
 , means that there are some restrictions on the forms of the functions
, means that there are some restrictions on the forms of the functions 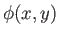 and
and 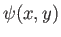 in
Equation (6.8).
Suppose that we approach
in
Equation (6.8).
Suppose that we approach  along the real axis, so that
along the real axis, so that
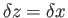 .
We obtain
.
We obtain
Suppose that we now approach  along the imaginary axis, so that
along the imaginary axis, so that
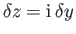 . We get
. We get
But, if  is a well-behaved function then its derivative must be
well-defined,
which implies that the previous two expressions are equivalent. This
requires that
is a well-behaved function then its derivative must be
well-defined,
which implies that the previous two expressions are equivalent. This
requires that
These expressions are called the Cauchy-Riemann relations, and are, in fact, sufficient to ensure
that all possible ways of taking the limit (6.13) give the same result (Riley 1974).
The Cauchy-Riemann relations can be combined to give
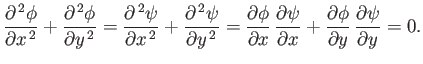 |
(6.19) |
In other words,
It follows that the real and imaginary parts of a well-behaved function of the complex variable both satisfy Laplace's
equation. Furthermore, the contours of these functions cross at right-angles.



Next: Complex Velocity Potential
Up: Two-Dimensional Potential Flow
Previous: Complex Functions
Richard Fitzpatrick
2016-03-31


![]() , means that there are some restrictions on the forms of the functions
, means that there are some restrictions on the forms of the functions ![]() and
and ![]() in
Equation (6.8).
Suppose that we approach
in
Equation (6.8).
Suppose that we approach ![]() along the real axis, so that
along the real axis, so that
![]() .
We obtain
.
We obtain