


Next: Cauchy-Riemann Relations
Up: Two-Dimensional Potential Flow
Previous: Introduction
The complex variable is conventionally written
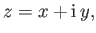 |
(6.1) |
where  represents the square root of minus one. Here,
represents the square root of minus one. Here,  and
and  are both real, and are identified with the corresponding
Cartesian coordinates.
(Incidentally,
are both real, and are identified with the corresponding
Cartesian coordinates.
(Incidentally,  should not be confused with a
should not be confused with a  -coordinate: this is a strictly two-dimensional discussion.)
We can also write
-coordinate: this is a strictly two-dimensional discussion.)
We can also write
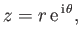 |
(6.2) |
where
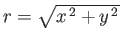 and
and
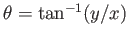 are the modulus and
argument of
are the modulus and
argument of  , respectively, but can also be identified with the corresponding plane polar coordinates.
Finally, Euler's theorem (Riley 1974),
, respectively, but can also be identified with the corresponding plane polar coordinates.
Finally, Euler's theorem (Riley 1974),
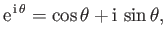 |
(6.3) |
implies that
We can define functions of the complex variable,  , in the same way that we
define functions of a real variable. For instance,
, in the same way that we
define functions of a real variable. For instance,
For a given function,  , we can substitute
, we can substitute
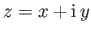 and write
and write
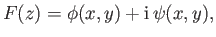 |
(6.8) |
where 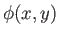 and
and 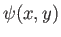 are real two-dimensional functions. Thus, if
are real two-dimensional functions. Thus, if
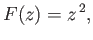 |
(6.9) |
then
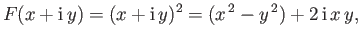 |
(6.10) |
giving



Next: Cauchy-Riemann Relations
Up: Two-Dimensional Potential Flow
Previous: Introduction
Richard Fitzpatrick
2016-03-31
![]() , in the same way that we
define functions of a real variable. For instance,
, in the same way that we
define functions of a real variable. For instance,