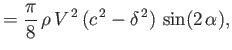Next: Zhukovskii's Hypothesis
Up: Incompressible Aerodynamics
Previous: Theorem of Kutta and
Cylindrical Airfoils
For the moment, let us work in the complex 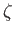 -plane, where
-plane, where
 .
Consider a cylindrical airfoil with a circular cross-section of radius
.
Consider a cylindrical airfoil with a circular cross-section of radius  , centered on the origin, that is situated in a uniform, high Reynolds number wind of speed
, centered on the origin, that is situated in a uniform, high Reynolds number wind of speed  whose direction
subtends a (clockwise) angle
whose direction
subtends a (clockwise) angle  with the negative
with the negative 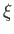 -axis. Let
-axis. Let
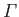 be the circulation of air around the airfoil. A slight generalization of the analysis of Section 6.4 reveals that the
appropriate complex velocity potential is
be the circulation of air around the airfoil. A slight generalization of the analysis of Section 6.4 reveals that the
appropriate complex velocity potential is
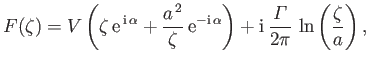 |
(9.14) |
whereas the associated stream function takes the form
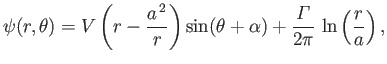 |
(9.15) |
where
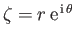 . It follows that
. It follows that
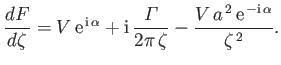 |
(9.16) |
Comparison with Equation (9.6) (with 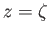 ) reveals that
) reveals that
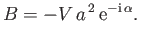 |
(9.17) |
Hence, Equations (9.10) and (9.13) yield
where 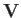 is the wind vector,
is the wind vector, 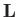 the lift vector, and
the lift vector, and 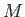 the moment of the lift vector about the
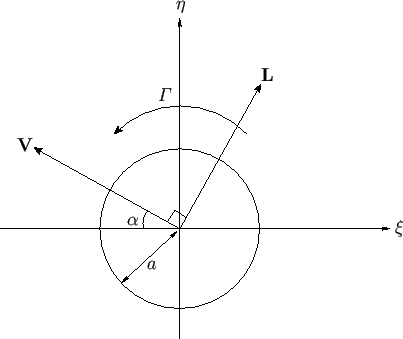
origin. We conclude that, for a cylindrical airfoil of circular cross-section, the lift vector is normal to the wind vector, and the line of action of the lift passes through the centroid of the cross-section (because the lift generates zero moment about the origin). (See Figure 9.1.)
the moment of the lift vector about the
origin. We conclude that, for a cylindrical airfoil of circular cross-section, the lift vector is normal to the wind vector, and the line of action of the lift passes through the centroid of the cross-section (because the lift generates zero moment about the origin). (See Figure 9.1.)
Figure 9.1:
A cylindrical airfoil of circular cross-section.
 |
Of course, a cylindrical airfoil of circular cross-section is completely unrealistic, because its back side (i.e., the side opposite to that from which the wind is incident) is not sufficiently
streamlined to prevent boundary layer separation. (See Chapter 8.) However, as described in Section 6.7, we can use the conformal transformation
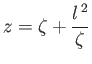 |
(9.21) |
to transform a cylinder of circular cross-section in the 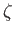 -plane to a cylinder of elliptical cross-section in the
-plane to a cylinder of elliptical cross-section in the  -plane. (Note that
both cross-sections have centroids located at the
origin.)
Moreover, a cylindrical airfoil of elliptical cross-section that is sufficiently elongated, and whose major axis subtends a sufficiently
small angle with the incident wind direction, constitutes a realistic airfoil, because its back side is, for the most part, closely
aligned with the external flow.
-plane. (Note that
both cross-sections have centroids located at the
origin.)
Moreover, a cylindrical airfoil of elliptical cross-section that is sufficiently elongated, and whose major axis subtends a sufficiently
small angle with the incident wind direction, constitutes a realistic airfoil, because its back side is, for the most part, closely
aligned with the external flow.
Figure 9.2:
A cylindrical airfoil of elliptical cross-section.
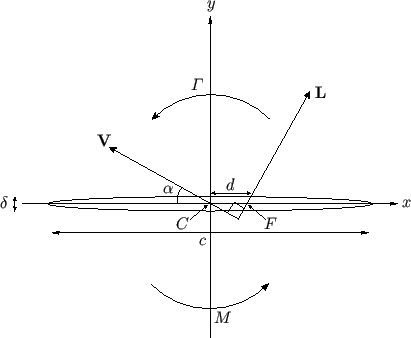 |
An elliptical airfoil of width 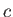 and thickness
and thickness 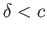 , as shown in Figure 9.2, is obtained when
the parameters
, as shown in Figure 9.2, is obtained when
the parameters  and
and 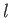 are given the following values:
are given the following values:
In this case, the surface of the airfoil satisfies the parametric equations
In particular, the airfoil's leading and trailing edges correspond to 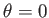 and
and
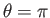 , respectively.
, respectively.
According to Equations (9.16) and (9.21), the complex velocity in the  -plane is given by
-plane is given by
![$\displaystyle \frac{dF}{dz} = \frac{dF}{d\zeta}\,\frac{d\zeta}{dz} = \left[V\,{...
...lpha}}{\zeta^{\,2}}\right]\left(\frac{\zeta^{\,2}}{\zeta^{\,2}-l^{\,2}}\right).$](img3311.png) |
(9.26) |
Thus, on the airfoil surface, where
 , we obtain
, we obtain
![$\displaystyle \frac{dF}{dz} = {\rm i}\left[V\,\sin(\alpha+\theta) + \frac{{\mit...
...ight]\frac{(c+\delta)}{\left(\delta\,\cos\theta+{\rm i}\,c\,\sin\theta\right)}.$](img3313.png) |
(9.27) |
A long way from the airfoil,
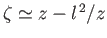 , so that Equation (9.26) reduces to
, so that Equation (9.26) reduces to
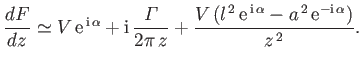 |
(9.28) |
A comparison with Equation (9.6) reveals that the circulation of air around the airfoil takes the same value,
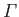 , in
both the complex
, in
both the complex 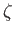 - and
- and  -planes. In other words, the conformal transformation (9.21) does not modify the circulation. The
transformation also does not modify the external wind speed or direction [because, from (9.16) and (9.28),
-planes. In other words, the conformal transformation (9.21) does not modify the circulation. The
transformation also does not modify the external wind speed or direction [because, from (9.16) and (9.28),
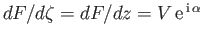 at
very large
at
very large  and
and 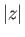 ]. On the
other hand, it is clear that the constant
]. On the
other hand, it is clear that the constant 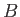 , which takes the value zero in the complex
, which takes the value zero in the complex 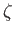 -plane, takes the value
-plane, takes the value
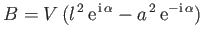 |
(9.29) |
in the complex  -plane.
Hence, Equations (9.10) and (9.13) reveal that
-plane.
Hence, Equations (9.10) and (9.13) reveal that
where 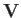 is the wind vector,
is the wind vector, 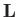 the lift vector, and
the lift vector, and 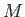 the moment of the lift vector about the
origin. Here,
the moment of the lift vector about the
origin. Here,
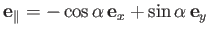 |
(9.33) |
is a unit vector parallel to the incident wind direction, and
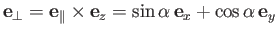 |
(9.34) |
is a unit vector perpendicular to the wind direction.
We conclude that, for a cylindrical airfoil of elliptic cross-section, the lift vector is normal to the wind vector, but the line of action of the lift intersects the major axis of the airfoil a distance
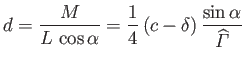 |
(9.35) |
in front of the cross-section's centroid,  , where
, where
![$ \widehat{\mit\Gamma}= {\mit\Gamma}/[\pi\,V\,(c+\delta)]$](img3324.png) . (See Figure 9.2.) Incidentally, the point,
. (See Figure 9.2.) Incidentally, the point, 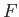 , at which the line of action of the
lift intersects the airfoil's major axis is conventionally termed the focus of the airfoil.
, at which the line of action of the
lift intersects the airfoil's major axis is conventionally termed the focus of the airfoil.



Next: Zhukovskii's Hypothesis
Up: Incompressible Aerodynamics
Previous: Theorem of Kutta and
Richard Fitzpatrick
2016-03-31
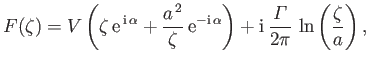
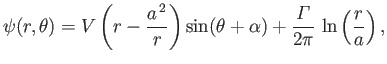
![]() and thickness
and thickness ![]() , as shown in Figure 9.2, is obtained when
the parameters
, as shown in Figure 9.2, is obtained when
the parameters ![]() and
and ![]() are given the following values:
are given the following values:

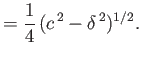
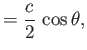
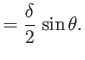
![]() -plane is given by
-plane is given by