


Next: Exercises
Up: Incompressible Viscous Flow
Previous: Axisymmetric Stokes Flow Around
Suppose that the solid sphere discussed in the previous section is replaced by a spherical fluid drop of radius 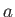 . Let the drop
move through the surrounding fluid at the constant velocity
. Let the drop
move through the surrounding fluid at the constant velocity
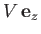 . Obviously, the
fluid from which the drop is composed must be immiscible with the surrounding fluid. Let us transform to
a frame of reference in which the drop is stationary, and centered at the origin.
Assuming that the Reynolds numbers immediately outside and inside
the drop are both much less than unity, and making use of the previous analysis, the
most general expressions for the stream function outside and inside the drop are
. Obviously, the
fluid from which the drop is composed must be immiscible with the surrounding fluid. Let us transform to
a frame of reference in which the drop is stationary, and centered at the origin.
Assuming that the Reynolds numbers immediately outside and inside
the drop are both much less than unity, and making use of the previous analysis, the
most general expressions for the stream function outside and inside the drop are
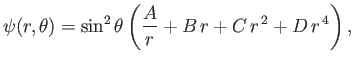 |
(10.135) |
and
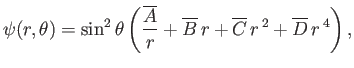 |
(10.136) |
respectively. Here, 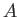 ,
, 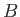 ,
, 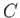 , et cetera, are arbitrary constants. Likewise, the previous analysis also allows us to deduce that
, et cetera, are arbitrary constants. Likewise, the previous analysis also allows us to deduce that
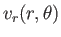 |
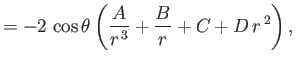 |
(10.137) |
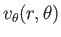 |
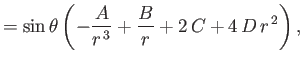 |
(10.138) |
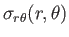 |
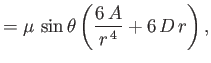 |
(10.139) |
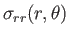 |
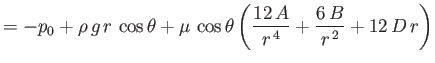 |
(10.140) |
in the region 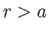 , with analogous expressions in the region
, with analogous expressions in the region 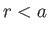 . Here,
. Here,  ,
,  ,
, 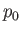 are the viscosity, density, and ambient
pressure of the fluid surrounding the drop. Let
are the viscosity, density, and ambient
pressure of the fluid surrounding the drop. Let
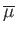 ,
,
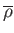 , and
, and
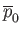 be the corresponding quantities
for the fluid that makes up the drop.
be the corresponding quantities
for the fluid that makes up the drop.
In the region outside the drop, the fluid velocity must asymptote to
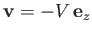 at large
at large 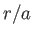 . This implies that
. This implies that
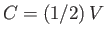 and
and  . Furthermore,
. Furthermore,
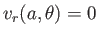 --that is, the normal velocity at the drop boundary must be zero--otherwise, the
drop would change shape. This constraint yields
--that is, the normal velocity at the drop boundary must be zero--otherwise, the
drop would change shape. This constraint yields
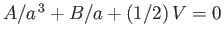 .
.
Inside the drop, the fluid velocity must remain finite as
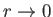 . This implies that
. This implies that
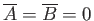 .
Furthermore, we again require that
.
Furthermore, we again require that
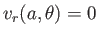 , which yields
, which yields
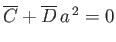 .
.
Two additional physical constraints that must be satisfied at the interface between the two fluids are, firstly, continuity of tangential
velocity--that is,
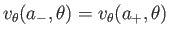 --and, secondly, continuity of tangential stress--that is,
--and, secondly, continuity of tangential stress--that is,
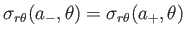 . These constraints yield
. These constraints yield
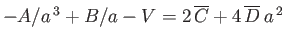 and
and
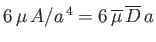 , respectively.
, respectively.
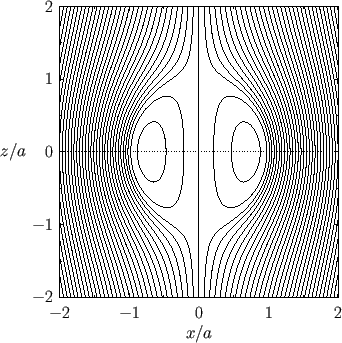
Figure:
Contours of the Stokes stream function in the  -
- plane for Stokes flow in and around a fluid sphere. Here,
plane for Stokes flow in and around a fluid sphere. Here,
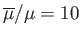 .
.
 |
At this stage, we have enough information to determine the values of 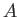 ,
, 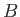 ,
,
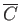 , and
, and
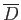 . In fact, the
stream functions outside and inside the drop can be shown to take the form
. In fact, the
stream functions outside and inside the drop can be shown to take the form
![$\displaystyle \psi(r,\theta) =\frac{1}{4}\,V\,a^2\,\sin^2\theta\left[\left(\fra...
...u}}{\mu+\overline{\mu}}\right)\frac{r}{a} + 2\left(\frac{r}{a}\right)^2\right],$](img3853.png) |
(10.141) |
and
![$\displaystyle \psi(r,\theta) = \frac{1}{4}\,V\,a^2\,\sin^2\theta\left(\frac{\mu...
...mu}}\right)\left(\frac{r}{a}\right)^2\left[1-\left(\frac{r}{a}\right)^2\right],$](img3854.png) |
(10.142) |
respectively. (See Figures 10.7 and 10.8.)
Figure:
Contours of the Stokes stream function in the  -
- plane for Stokes flow in and around a fluid sphere. Here,
plane for Stokes flow in and around a fluid sphere. Here,
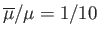 .
.
 |
The discontinuity in the radial stress across the drop boundary is
The final physical constraint that must be satisfied at  is
is
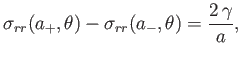 |
(10.144) |
where 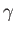 is the surface tension of the interface between the two fluids. (See Section 3.3.)
Hence, we obtain
is the surface tension of the interface between the two fluids. (See Section 3.3.)
Hence, we obtain
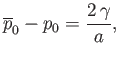 |
(10.145) |
and
![$\displaystyle V = \frac{a^{\,2}\,g}{3\,\nu}\,\left(1-\frac{\overline{\rho}}{\rho}\right)\left[\frac{\mu+\overline{\mu}}{\mu+(3/2)\,\overline{\mu}}\right],$](img3861.png) |
(10.146) |
where
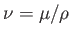 is the kinematic viscosity of the surrounding fluid.
The fact that we have been able to completely satisfy all of the physical constraints at the interface between the two fluids,
as long as the drop moves at the constant vertical velocity
is the kinematic viscosity of the surrounding fluid.
The fact that we have been able to completely satisfy all of the physical constraints at the interface between the two fluids,
as long as the drop moves at the constant vertical velocity  , proves that our previous assumptions that the interface
is spherical, and that the drop moves vertically through the surrounding fluid at a constant speed without changing shape, were correct.
In the limit,
, proves that our previous assumptions that the interface
is spherical, and that the drop moves vertically through the surrounding fluid at a constant speed without changing shape, were correct.
In the limit,
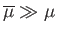 , in which the drop is much more viscous than the surrounding fluid, we
recover Equation (10.128): that is, the drop acts like a solid sphere. On the other hand, in the limit
, in which the drop is much more viscous than the surrounding fluid, we
recover Equation (10.128): that is, the drop acts like a solid sphere. On the other hand, in the limit
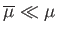 , and
, and
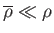 , which is appropriate to an air bubble rising through a liquid, we obtain
, which is appropriate to an air bubble rising through a liquid, we obtain
 |
(10.147) |



Next: Exercises
Up: Incompressible Viscous Flow
Previous: Axisymmetric Stokes Flow Around
Richard Fitzpatrick
2016-01-22
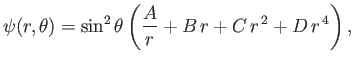
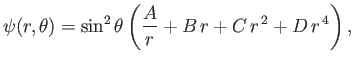
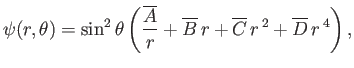
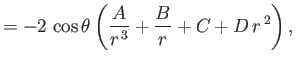
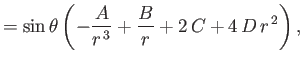
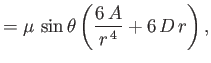
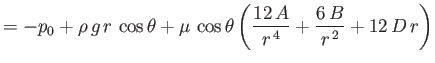
![]() at large
at large ![]() . This implies that
. This implies that
![]() and
and ![]() . Furthermore,
. Furthermore,
![]() --that is, the normal velocity at the drop boundary must be zero--otherwise, the
drop would change shape. This constraint yields
--that is, the normal velocity at the drop boundary must be zero--otherwise, the
drop would change shape. This constraint yields
![]() .
.
![]() . This implies that
. This implies that
![]() .
Furthermore, we again require that
.
Furthermore, we again require that
![]() , which yields
, which yields
![]() .
.
![]() --and, secondly, continuity of tangential stress--that is,
--and, secondly, continuity of tangential stress--that is,
![]() . These constraints yield
. These constraints yield
![]() and
and
![]() , respectively.
, respectively.

![]() ,
, ![]() ,
,
![]() , and
, and
![]() . In fact, the
stream functions outside and inside the drop can be shown to take the form
. In fact, the
stream functions outside and inside the drop can be shown to take the form
![$\displaystyle \psi(r,\theta) =\frac{1}{4}\,V\,a^2\,\sin^2\theta\left[\left(\fra...
...u}}{\mu+\overline{\mu}}\right)\frac{r}{a} + 2\left(\frac{r}{a}\right)^2\right],$](img3853.png)
![$\displaystyle \psi(r,\theta) = \frac{1}{4}\,V\,a^2\,\sin^2\theta\left(\frac{\mu...
...mu}}\right)\left(\frac{r}{a}\right)^2\left[1-\left(\frac{r}{a}\right)^2\right],$](img3854.png)

![$\displaystyle \phantom{=}- 3\,\mu\,\frac{V}{a}\left[\frac{\mu+(3/2)\,\overline{\mu}}{\mu+\overline{\mu}}\right]\cos\theta.$](img3858.png)
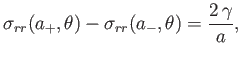
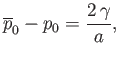
![$\displaystyle V = \frac{a^{\,2}\,g}{3\,\nu}\,\left(1-\frac{\overline{\rho}}{\rho}\right)\left[\frac{\mu+\overline{\mu}}{\mu+(3/2)\,\overline{\mu}}\right],$](img3861.png)
