Next: Capillary Length
Up: Surface Tension
Previous: Young-Laplace Equation
Spherical Interfaces
Generally speaking, the equilibrium shape of an interface between two immiscible fluids is determined by solving
the force balance equation (2.1) in each fluid, and then applying the Young-Laplace equation to the
interface. However, in situations in which a mass of one fluid is completely
immersed in a second fluid--for example, a mist droplet in air, or a gas bubble in water--the shape of the interface is fairly obvious. Provided that either the
size of the droplet or bubble, or the difference in densities on the two sides of the interface, is sufficiently small,
we can safely ignore the effect of gravity. This implies that the pressure is uniform in each fluid, and consequently that the pressure jump
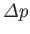 is constant over the interface. Hence, from Equation (3.12), the mean curvature
is constant over the interface. Hence, from Equation (3.12), the mean curvature
 of the interface is also constant. Because a sphere is the only closed surface which possesses a constant mean curvature, we conclude that
the interface is spherical. This result also follows from the argument that a stable equilibrium state
is one which minimizes the free energy of the interface, subject to the constraint that the enclosed volume be
constant. Thus, the equilibrium shape of the interface is that which
has the least surface area for a given volume: in other words, a sphere.
of the interface is also constant. Because a sphere is the only closed surface which possesses a constant mean curvature, we conclude that
the interface is spherical. This result also follows from the argument that a stable equilibrium state
is one which minimizes the free energy of the interface, subject to the constraint that the enclosed volume be
constant. Thus, the equilibrium shape of the interface is that which
has the least surface area for a given volume: in other words, a sphere.
Suppose that the interface corresponds to the spherical surface  , where
, where 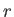 is a spherical coordinate. (See Section C.4.)
It follows that
is a spherical coordinate. (See Section C.4.)
It follows that
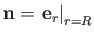 . (Note, for future reference, that
. (Note, for future reference, that 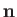 points away from the center of
curvature of the interface.)
Hence, from Equation (C.65),
points away from the center of
curvature of the interface.)
Hence, from Equation (C.65),
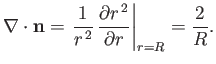 |
(3.13) |
The Young-Laplace equation, (3.12), then gives
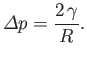 |
(3.14) |
Thus, given that
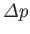 is the pressure jump seen crossing the interface in the opposite direction to
is the pressure jump seen crossing the interface in the opposite direction to 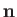 ,
we conclude that the
pressure inside a droplet or bubble exceeds that outside by an amount proportional to the surface tension, and
inversely proportional to the droplet or bubble radius. This explains why small bubbles are louder that large
ones when they burst at a free surface: for instance, champagne fizzes louder than beer. Note that soap bubbles in air
have two interfaces defining the inner and outer extents of the soap film. Consequently, the net pressure difference is
twice that across a single interface.
,
we conclude that the
pressure inside a droplet or bubble exceeds that outside by an amount proportional to the surface tension, and
inversely proportional to the droplet or bubble radius. This explains why small bubbles are louder that large
ones when they burst at a free surface: for instance, champagne fizzes louder than beer. Note that soap bubbles in air
have two interfaces defining the inner and outer extents of the soap film. Consequently, the net pressure difference is
twice that across a single interface.



Next: Capillary Length
Up: Surface Tension
Previous: Young-Laplace Equation
Richard Fitzpatrick
2016-01-22
![]() , where
, where ![]() is a spherical coordinate. (See Section C.4.)
It follows that
is a spherical coordinate. (See Section C.4.)
It follows that
![]() . (Note, for future reference, that
. (Note, for future reference, that ![]() points away from the center of
curvature of the interface.)
Hence, from Equation (C.65),
points away from the center of
curvature of the interface.)
Hence, from Equation (C.65),