


Next: Axisymmetric Stokes Flow In
Up: Incompressible Viscous Flow
Previous: Axisymmetric Stokes Flow
Consider a solid sphere of radius 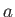 that is moving under gravity at the constant vertical velocity
that is moving under gravity at the constant vertical velocity
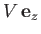 through a stationary fluid of
density
through a stationary fluid of
density  and viscosity
and viscosity  . Here, gravitational acceleration is assumed to take the form
. Here, gravitational acceleration is assumed to take the form
 . Provided that the typical Reynolds number,
. Provided that the typical Reynolds number,
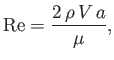 |
(10.94) |
is much less than unity, the flow around the sphere is an example of axisymmetric Stokes flow. Let us transform to a frame of
reference in which the sphere is stationary, and centered at the origin. Adopting the standard spherical coordinates 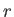 ,
, 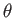 ,
, 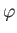 ,
the surface of the sphere corresponds to
,
the surface of the sphere corresponds to  , and the surrounding fluid occupies the region
, and the surrounding fluid occupies the region 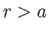 . By symmetry, the flow
field outside the sphere is axisymmetric (i.e.,
. By symmetry, the flow
field outside the sphere is axisymmetric (i.e.,
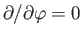 ), and has no toroidal component
(i.e.,
), and has no toroidal component
(i.e.,
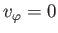 ). The physical boundary conditions at the surface of the sphere are
). The physical boundary conditions at the surface of the sphere are
that is, the normal and tangential fluid velocities are both zero at the surface. A long way from the sphere, we expect the
fluid velocity to asymptote to
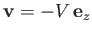 . In other words,
. In other words,
Let us write
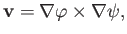 |
(10.99) |
where
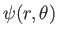 is the Stokes stream function. As we saw in the previous section, axisymmetric Stokes flow is characterized by
is the Stokes stream function. As we saw in the previous section, axisymmetric Stokes flow is characterized by
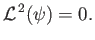 |
(10.100) |
Here, the differential operator 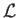 is specified in Equation (10.88). The boundary conditions (10.95)-(10.98) reduce to
is specified in Equation (10.88). The boundary conditions (10.95)-(10.98) reduce to
Equation (10.103) suggests that
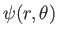 can be written in the separable form
can be written in the separable form
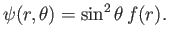 |
(10.104) |
In this case,
and Equations (10.100)-(10.103) reduce to
Figure:
Contours of the stream function  in the
in the  -
- plane for Stokes flow around a solid sphere.
plane for Stokes flow around a solid sphere.
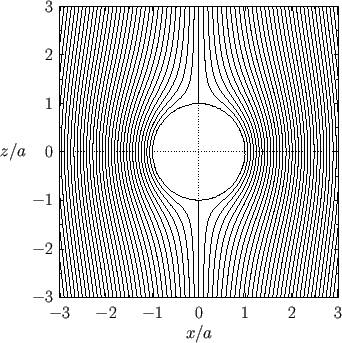 |
Let us try a test solution to Equation (10.107) of the form
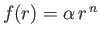 . We find that
. We find that
![$\displaystyle \alpha\left[n\,(n-1)-2\right]\,[(n-2)\,(n-3)-2] = 0,$](img3771.png) |
(10.110) |
which implies that 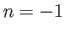 ,
,  ,
,  ,
,  . Hence, the most general solution to Equation (10.107) is
. Hence, the most general solution to Equation (10.107) is
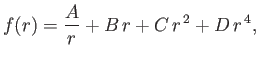 |
(10.111) |
where 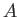 ,
, 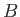 ,
, 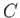 ,
, 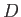 are arbitrary constants. However, the boundary condition (10.109)
yields
are arbitrary constants. However, the boundary condition (10.109)
yields
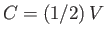 and
and  , whereas the boundary condition (10.108) gives
, whereas the boundary condition (10.108) gives
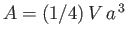 and
and
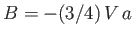 . Thus, we conclude that
. Thus, we conclude that
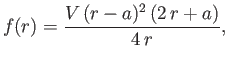 |
(10.112) |
and the stream function becomes
 |
(10.113) |
(See Figure 10.4.)
From Equation (10.87), the fluid vorticity is
 |
(10.114) |
(See Figure 10.5.)
Moreover, from Equation (10.81),
Hence,
which implies that the effective pressure distribution within the fluid is
 |
(10.118) |
where  is an arbitrary constant. (See Figure 10.6.) However,
is an arbitrary constant. (See Figure 10.6.) However,
 , where
, where
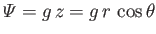 . Thus,
the actual pressure distribution is
. Thus,
the actual pressure distribution is
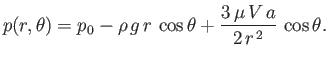 |
(10.119) |
Figure:
Contours of the vorticity,
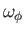 , in the
, in the  -
- plane for Stokes flow around a solid sphere. Solid/dashed lines
correspond to opposite signs of
plane for Stokes flow around a solid sphere. Solid/dashed lines
correspond to opposite signs of
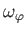 .
.
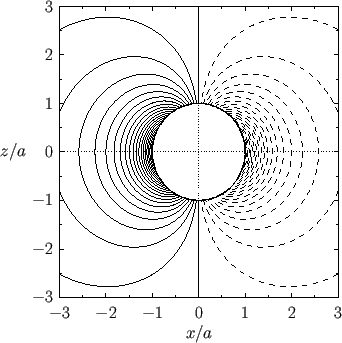 |
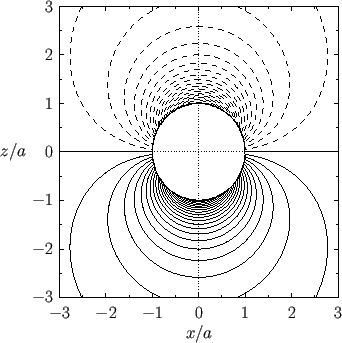
Figure:
Contours of the effective pressure,  , in the
, in the  -
- plane for Stokes flow around a solid sphere. Solid/dashed lines
correspond to opposite signs of
plane for Stokes flow around a solid sphere. Solid/dashed lines
correspond to opposite signs of  .
.
 |
From Section 1.20, the radial and tangential components of the force per unit area exerted on the
sphere by the fluid are
Now,
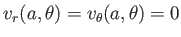 . Moreover, because
. Moreover, because
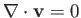 , it follows from Equation (1.168) that
, it follows from Equation (1.168) that
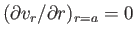 .
Finally, Equation (10.87) yields
.
Finally, Equation (10.87) yields
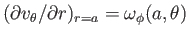 . Hence,
. Hence,
Thus, the force density at the surface of the sphere is
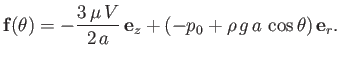 |
(10.124) |
It follows that the net vertical force exerted on the sphere by the fluid is
which reduces to
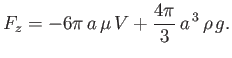 |
(10.126) |
By symmetry, the horizontal components of the net force both average to zero. We can recognize the second term on the right-hand
side of the previous equation as the buoyancy force due to the weight of the fluid displaced by the sphere. (See Chapter 2.) Moreover, the first term can be
interpreted as the viscous drag acting
on the sphere. Note that this drag acts in the opposite direction to the relative
motion of the sphere with respect to the fluid, and its magnitude is directly proportional to the relative velocity.
Vertical force balance requires that
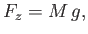 |
(10.127) |
where 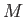 is the sphere's mass. In other words, in a steady state, the weight of the sphere balances the
vertical force exerted by the surrounding fluid. If the sphere is composed of material of mean density
is the sphere's mass. In other words, in a steady state, the weight of the sphere balances the
vertical force exerted by the surrounding fluid. If the sphere is composed of material of mean density
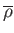 then
then
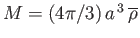 . Hence, in the frame in which the fluid a large distance from the sphere is stationary, the steady vertical velocity with which the sphere moves through the fluid is
. Hence, in the frame in which the fluid a large distance from the sphere is stationary, the steady vertical velocity with which the sphere moves through the fluid is
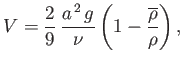 |
(10.128) |
where
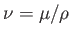 is the fluid's kinematic viscosity. Obviously, if the sphere is more dense than the fluid (i.e., if
is the fluid's kinematic viscosity. Obviously, if the sphere is more dense than the fluid (i.e., if
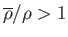 ) then it moves downward (i.e.,
) then it moves downward (i.e., 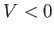 ), and vice versa. Finally, the typical Reynolds number of the fluid flow in the vicinity of the sphere is
), and vice versa. Finally, the typical Reynolds number of the fluid flow in the vicinity of the sphere is
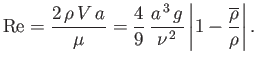 |
(10.129) |
For the case of a grain of sand falling through water at
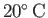 , we have
, we have
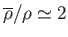 and
and
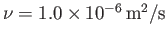 (Batchelor 2000).
Hence,
(Batchelor 2000).
Hence,
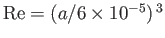 , where
, where 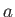 is measured in meters. Thus, expression (10.128), which is strictly speaking
only valid when
is measured in meters. Thus, expression (10.128), which is strictly speaking
only valid when
 , but which turns out to be approximately valid for all Reynolds numbers less than unity,
only holds for sand grains whose radii are less than about
, but which turns out to be approximately valid for all Reynolds numbers less than unity,
only holds for sand grains whose radii are less than about 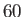 microns. Such grains fall through water at approximately
microns. Such grains fall through water at approximately
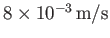 . For the case of a droplet of water falling through air at
. For the case of a droplet of water falling through air at
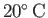 and atmospheric pressure, we have
and atmospheric pressure, we have
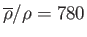 and
and
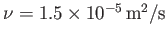 (Batchelor 2000).
Hence,
(Batchelor 2000).
Hence,
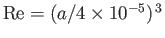 , where
, where 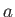 is measured in meters. Thus, expression (10.128)
only holds for water droplets whose radii are less than about
is measured in meters. Thus, expression (10.128)
only holds for water droplets whose radii are less than about  microns. Such droplets fall through air at approximately
microns. Such droplets fall through air at approximately
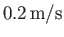 .
.
At large values of 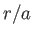 , Equations (10.105), (10.106), and (10.112) yield
, Equations (10.105), (10.106), and (10.112) yield
It follows that
![$\displaystyle [\rho\,({\bf v}\cdot\nabla)\,{\bf v}]_r = \rho\left(v_r\,\frac{\p...
...\theta}- \frac{v_\theta^{\,2}}{r}\right) \sim \frac{\rho\,V^{\,2}\,a}{r^{\,2}},$](img3826.png) |
(10.132) |
and
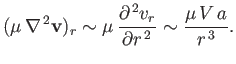 |
(10.133) |
Hence,
![$\displaystyle \frac{[\rho\,({\bf v}\cdot\nabla)\,{\bf v}]_r }{(\mu\,\nabla^2{\bf v})_r} \sim \frac{\rho\,V\,r}{\mu}\sim {\rm Re}\left(\frac{r}{a}\right),$](img3828.png) |
(10.134) |
where 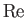 is the Reynolds number of the flow in the immediate vicinity of the sphere. [See Equation (10.94).]
Our analysis is based on the assumption that advective inertia is negligible with respect to viscosity. However, as is clear from the
previous expression for the ratio of inertia to viscosity within the fluid, even if this ratio is much less than unity close to
the sphere--in other words, if
is the Reynolds number of the flow in the immediate vicinity of the sphere. [See Equation (10.94).]
Our analysis is based on the assumption that advective inertia is negligible with respect to viscosity. However, as is clear from the
previous expression for the ratio of inertia to viscosity within the fluid, even if this ratio is much less than unity close to
the sphere--in other words, if
 --it inevitably becomes much greater than unity far from the
sphere: that is, for
--it inevitably becomes much greater than unity far from the
sphere: that is, for
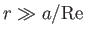 . In other words, inertia always dominates viscosity, and our Stokes flow solution therefore breaks down, at sufficiently large
. In other words, inertia always dominates viscosity, and our Stokes flow solution therefore breaks down, at sufficiently large 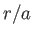 .
.



Next: Axisymmetric Stokes Flow In
Up: Incompressible Viscous Flow
Previous: Axisymmetric Stokes Flow
Richard Fitzpatrick
2016-01-22
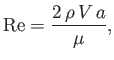
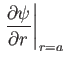
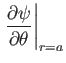
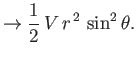
![]() can be written in the separable form
can be written in the separable form
![]() . We find that
. We find that
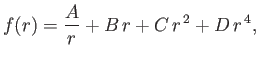

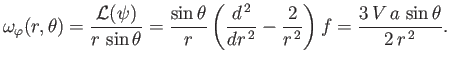

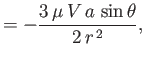
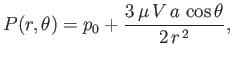
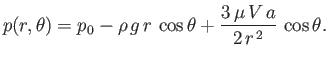


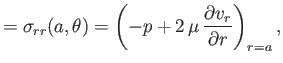
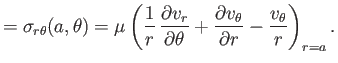
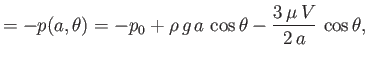
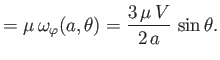
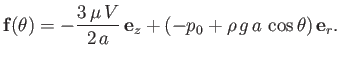
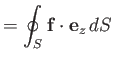
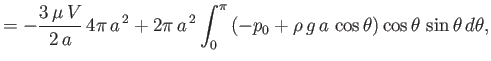
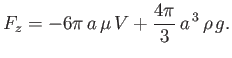
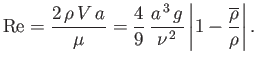
![]() , we have
, we have
![]() and
and
![]() (Batchelor 2000).
Hence,
(Batchelor 2000).
Hence,
![]() , where
, where ![]() is measured in meters. Thus, expression (10.128), which is strictly speaking
only valid when
is measured in meters. Thus, expression (10.128), which is strictly speaking
only valid when
![]() , but which turns out to be approximately valid for all Reynolds numbers less than unity,
only holds for sand grains whose radii are less than about
, but which turns out to be approximately valid for all Reynolds numbers less than unity,
only holds for sand grains whose radii are less than about ![]() microns. Such grains fall through water at approximately
microns. Such grains fall through water at approximately
![]() . For the case of a droplet of water falling through air at
. For the case of a droplet of water falling through air at
![]() and atmospheric pressure, we have
and atmospheric pressure, we have
![]() and
and
![]() (Batchelor 2000).
Hence,
(Batchelor 2000).
Hence,
![]() , where
, where ![]() is measured in meters. Thus, expression (10.128)
only holds for water droplets whose radii are less than about
is measured in meters. Thus, expression (10.128)
only holds for water droplets whose radii are less than about ![]() microns. Such droplets fall through air at approximately
microns. Such droplets fall through air at approximately
![]() .
.
![]() , Equations (10.105), (10.106), and (10.112) yield
, Equations (10.105), (10.106), and (10.112) yield
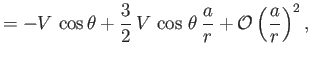
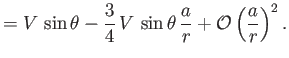
![$\displaystyle [\rho\,({\bf v}\cdot\nabla)\,{\bf v}]_r = \rho\left(v_r\,\frac{\p...
...\theta}- \frac{v_\theta^{\,2}}{r}\right) \sim \frac{\rho\,V^{\,2}\,a}{r^{\,2}},$](img3826.png)
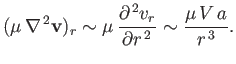
![$\displaystyle \frac{[\rho\,({\bf v}\cdot\nabla)\,{\bf v}]_r }{(\mu\,\nabla^2{\bf v})_r} \sim \frac{\rho\,V\,r}{\mu}\sim {\rm Re}\left(\frac{r}{a}\right),$](img3828.png)