Next: Single-Slit Diffraction Up: Wave Optics Previous: Thin-Film Interference Contents
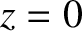 , in which a number of narrow (i.e.,
, in which a number of narrow (i.e.,
 ,
where
,
where 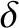 is the slit width) slits, running parallel to the
is the slit width) slits, running parallel to the  -axis, have been cut. Let us now generalize our analysis
to take slits of finite width (i.e.,
-axis, have been cut. Let us now generalize our analysis
to take slits of finite width (i.e.,
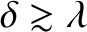 ) into account. In order to achieve this goal, it is convenient to
define the so-called aperture function,
) into account. In order to achieve this goal, it is convenient to
define the so-called aperture function, 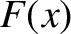 , of the screen. This function takes the value zero if the screen is
opaque at position
, of the screen. This function takes the value zero if the screen is
opaque at position  , and some constant positive value if it is transparent, and is normalized such that
, and some constant positive value if it is transparent, and is normalized such that
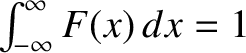 . Thus, for the case of a screen with
. Thus, for the case of a screen with  identical
slits of negligible width, located at
identical
slits of negligible width, located at 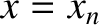 , for
, for 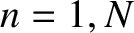 , the appropriate aperture function is
, the appropriate aperture function is
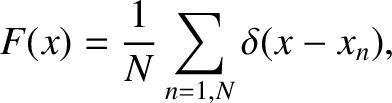 |
(10.49) |
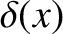 is a Dirac delta function.
is a Dirac delta function.
The wavefunction at the projection screen, generated by the previously mentioned arrangement of slits, when the opaque screen is
illuminated by a plane wave of phase angle  , wavenumber
, wavenumber  , and angular frequency
, and angular frequency  , whose
direction of propagation subtends an angle
, whose
direction of propagation subtends an angle 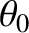 with the
with the  -axis, is (see the analysis in Sections 10.2 and 10.4)
-axis, is (see the analysis in Sections 10.2 and 10.4)
 , so that
, so that
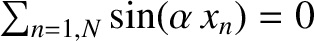 for any
for any 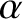 .
Using the well-known properties of the delta function [see Equation (8.26)], Equation (10.50) can also be written
where
In the following, we shall assume that Equation (10.51) is a general result, and is valid even when the
slits in the opaque screen are of finite width (i.e.,
.
Using the well-known properties of the delta function [see Equation (8.26)], Equation (10.50) can also be written
where
In the following, we shall assume that Equation (10.51) is a general result, and is valid even when the
slits in the opaque screen are of finite width (i.e.,
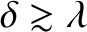 ). This assumption is equivalent to the assumption that each unblocked section of the screen emits a cylindrical wave in the forward direction that is in phase with
the plane wave which illuminates it from behind. The latter assumption is known as Huygen's principle.
Huygen's principle can be justified, with certain provisos (see Section 10.10), using electromagnetic
theory (Jackson 1975), but such a proof lies beyond the scope of this course.
The interference/diffraction function,
). This assumption is equivalent to the assumption that each unblocked section of the screen emits a cylindrical wave in the forward direction that is in phase with
the plane wave which illuminates it from behind. The latter assumption is known as Huygen's principle.
Huygen's principle can be justified, with certain provisos (see Section 10.10), using electromagnetic
theory (Jackson 1975), but such a proof lies beyond the scope of this course.
The interference/diffraction function,
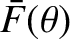 , is the Fourier transform of the aperture function,
, is the Fourier transform of the aperture function, 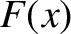 .
This is an extremely powerful result. It implies that we can calculate the far-field interference/diffraction pattern associated
with any arrangement of parallel slits, of arbitrary width, by Fourier transforming the associated aperture function. Once we have determined the interference/diffraction function,
.
This is an extremely powerful result. It implies that we can calculate the far-field interference/diffraction pattern associated
with any arrangement of parallel slits, of arbitrary width, by Fourier transforming the associated aperture function. Once we have determined the interference/diffraction function,
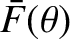 , the intensity of the
interference/diffraction pattern appearing on the projection screen is readily obtained from
, the intensity of the
interference/diffraction pattern appearing on the projection screen is readily obtained from
![$\displaystyle {\cal I}(\theta) \propto \left[\bar{F}(\theta)\right]^{\,2}.$](img3428.png) |
(10.53) |