Next: Diffraction from Straight Wire Up: Wave Optics Previous: Diffraction from Straight Edge Contents
![\includegraphics[width=1\textwidth]{Chapter10/fig10_18.eps}](img3653.png) |
Consider the diffraction pattern of a rectangular slit that runs parallel to the 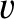 -axis
and extends from
-axis
and extends from
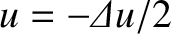 to
to
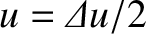 . In other words, let
. In other words, let
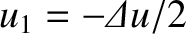 and
and
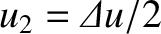 . It is easily demonstrated, from Equations (10.121), (10.122), (10.125), and (10.126), that
. It is easily demonstrated, from Equations (10.121), (10.122), (10.125), and (10.126), that
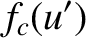 |
![$\displaystyle = \frac{1}{2}\left[C({\mit\Delta u}/2-u') + C(u'+{\mit\Delta u}/2)\right]
-\frac{1}{2}\left[S({\mit\Delta u}/2-u') + S(u'+{\mit\Delta u}/2)\right],$](img3658.png) |
(10.133) |
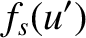 |
![$\displaystyle = \frac{1}{2}\left[C({\mit\Delta u}/2-u') + C(u'+{\mit\Delta u}/2)\right]
+\frac{1}{2}\left[S({\mit\Delta u}/2-u') + S(u'+{\mit\Delta u}/2)\right].$](img3659.png) |
(10.134) |
![$\displaystyle \frac{{\cal I}(u')}{{\cal I}_0 }= \frac{1}{2}\left[C({\mit\Delta ...
...
\frac{1}{2}\left[S({\mit\Delta u}/2-u') + S(u'+{\mit\Delta u}/2)\right]^{\,2}.$](img3660.png) |
(10.135) |
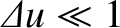 [see Equations (10.96) and
(10.98)], whereas the near-field limit
corresponds to
[see Equations (10.96) and
(10.98)], whereas the near-field limit
corresponds to
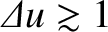 [see Equation (10.97)].
[see Equation (10.97)].
Figure 10.18 shows the diffraction pattern of a rectangular slit. It can be seen that in the
far-field limit,
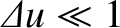 , the diffraction pattern is the same as that calculated in
Section 10.7. However, in the near-field limit,
, the diffraction pattern is the same as that calculated in
Section 10.7. However, in the near-field limit,
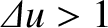 , the diffraction pattern is significantly
modified. For instance, in the far-field limit, the diffraction pattern is much wider than the slit, whereas, in the
near-field limit, the diffraction pattern is similar in size to the slit. In fact, in the
extreme near-field limit,
, the diffraction pattern is significantly
modified. For instance, in the far-field limit, the diffraction pattern is much wider than the slit, whereas, in the
near-field limit, the diffraction pattern is similar in size to the slit. In fact, in the
extreme near-field limit,
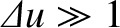 , the diffraction pattern is fairly similar in
form to the geometric image of the slit, apart from the presence of fringes within the image.
, the diffraction pattern is fairly similar in
form to the geometric image of the slit, apart from the presence of fringes within the image.