Next: Diffraction from Circular Aperture Up: Wave Optics Previous: Diffraction from Rectangular Slit Contents
![\includegraphics[width=1\textwidth]{Chapter10/fig10_19.eps}](img3665.png) |
Consider the diffraction pattern of a straight wire that runs parallel to the  -axis
and extends from
-axis
and extends from
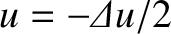 to
to
 . Because the wire is the complementary aperture of
the rectangular slit discussed in the previous section, we can use Babinet's principle (see Section 10.11)
to deduce that
. Because the wire is the complementary aperture of
the rectangular slit discussed in the previous section, we can use Babinet's principle (see Section 10.11)
to deduce that
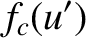 |
![$\displaystyle = -\frac{1}{2}\left[C({\mit\Delta u}/2-u') + C(u'+{\mit\Delta u}/...
...ight]
+\frac{1}{2}\left[S({\mit\Delta u}/2-u') + S(u'+{\mit\Delta u}/2)\right],$](img3666.png) |
(10.136) |
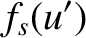 |
![$\displaystyle = 1-\frac{1}{2}\left[C({\mit\Delta u}/2-u') + C(u'+{\mit\Delta u}...
...ight]
-\frac{1}{2}\left[S({\mit\Delta u}/2-u') + S(u'+{\mit\Delta u}/2)\right].$](img3667.png) |
(10.137) |
Figure 10.19 shows the diffraction pattern of a straight wire. In the far-field limit,
 ,
the diffraction pattern consists of a bright spot, centered on the wire, surrounded by a
set of interference fringes. The fringes can be thought of as the interference pattern of the light
passing immediately to either side of the wire. In fact, if we think of the wire as two slits whose
spacing is the diameter of the wire then straightforward interference theory (see Section 10.2) suggests that the
fringe width should be
,
the diffraction pattern consists of a bright spot, centered on the wire, surrounded by a
set of interference fringes. The fringes can be thought of as the interference pattern of the light
passing immediately to either side of the wire. In fact, if we think of the wire as two slits whose
spacing is the diameter of the wire then straightforward interference theory (see Section 10.2) suggests that the
fringe width should be
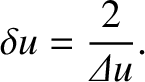 |
(10.138) |
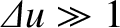 , the
diffraction pattern of the wire is essentially a geometric shadow, bounded on either side by a
straight-edge diffraction pattern. (See Section 10.13.)
, the
diffraction pattern of the wire is essentially a geometric shadow, bounded on either side by a
straight-edge diffraction pattern. (See Section 10.13.)