Consider a high-frequency, circularly polarized, electromagnetic wave propagating, along the 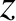 -axis, through
a plasma with a longitudinal equilibrium magnetic field of strength,
-axis, through
a plasma with a longitudinal equilibrium magnetic field of strength,
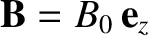 .
The equations of motion of an individual electron making up the plasma take the
form (see Appendix C)
where
.
The equations of motion of an individual electron making up the plasma take the
form (see Appendix C)
where 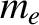 is the electron mass, and
is the electron mass, and 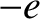 the electron charge.
Here,
the electron charge.
Here,  and
and  are the wave-induced displacements of the electron in the
are the wave-induced displacements of the electron in the  - and
- and  -directions, respectively.
(As before, it is a good approximation to neglect the wave-induced displacements of the ions, because of their relatively large mass.)
The former terms on the right-hand sides of the previous equations
represent the
-directions, respectively.
(As before, it is a good approximation to neglect the wave-induced displacements of the ions, because of their relatively large mass.)
The former terms on the right-hand sides of the previous equations
represent the  - and
- and  -directed forces exerted on the electron by the wave electric field,
-directed forces exerted on the electron by the wave electric field, 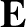 ,
whereas the latter terms represent the forces exerted by the equilibrium magnetic field when the electron moves (Fitzpatrick 2008).
(As before, we can neglect the forces due to the wave magnetic field, provided that the
electron motion remains non-relativistic.)
,
whereas the latter terms represent the forces exerted by the equilibrium magnetic field when the electron moves (Fitzpatrick 2008).
(As before, we can neglect the forces due to the wave magnetic field, provided that the
electron motion remains non-relativistic.)
Consider a right-hand circularly polarized wave, of angular frequency  , whose electric field takes the form
, whose electric field takes the form
(See Section 7.7.) Let us search for solutions of Equations (9.54) and (9.55) of the form
It is readily demonstrated (see Exercise 6) that
where
 |
(9.62) |
is the so-called electron cyclotron frequency at which the electrons gyrate in the equilibrium magnetic field (Stix 1962).
If 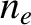 is the number density of electrons in the plasma then it follows that the
is the number density of electrons in the plasma then it follows that the  - and
- and  -components of the electric dipole moment per unit volume are
respectively. For the case of a circularly polarized wave, Equations (9.24) and (9.25) generalize to give (see Appendix C)
Thus, writing
-components of the electric dipole moment per unit volume are
respectively. For the case of a circularly polarized wave, Equations (9.24) and (9.25) generalize to give (see Appendix C)
Thus, writing 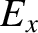 and
and  in the form (9.56) and (9.57), respectively,
the components of the magnetic intensity in the form
and
in the form (9.56) and (9.57), respectively,
the components of the magnetic intensity in the form
and 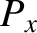 and
and 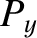 in the form (9.63) and (9.64), respectively, Equations (9.65)–(9.68)
yield the nonlinear dispersion relation
in the form (9.63) and (9.64), respectively, Equations (9.65)–(9.68)
yield the nonlinear dispersion relation
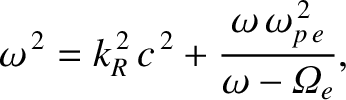 |
(9.71) |
where
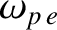 is the (electron) plasma frequency. [See Equation (9.28).] It follows that the refractive index of the plasma for right-hand circularly polarized waves is
is the (electron) plasma frequency. [See Equation (9.28).] It follows that the refractive index of the plasma for right-hand circularly polarized waves is
![$\displaystyle n_R = \frac{k_R\,c}{\omega} = \left[1-\frac{\omega_{p\,e}^{\,2}}{\omega\,(\omega-{\mit\Omega}_e)}\right]^{1/2},$](img2666.png) |
(9.72) |
whereas the effective impedance becomes
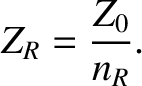 |
(9.73) |
Here,  is the impedance of free space.
is the impedance of free space.
Consider a left-hand circularly polarized wave whose electric field takes the form
(See Section 7.7.) Repeating the previous analysis (with suitable modifications), we deduce that the dispersion relation
for left-hand circularly polarized waves is
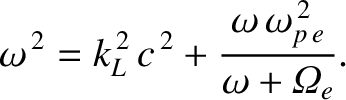 |
(9.76) |
It follows that the refractive index of the plasma for such waves is
![$\displaystyle n_L = \frac{k_L\,c}{\omega} = \left[1-\frac{\omega_{p\,e}^{\,2}}{\omega\,(\omega+{\mit\Omega}_e)}\right]^{1/2},$](img2671.png) |
(9.77) |
whereas the effective impedance becomes
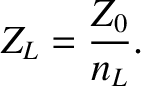 |
(9.78) |
According to the previous analysis, in the presence of a longitudinal equilibrium magnetic field, the refractive indices of
right-hand and left-hand circularly polarized electromagnetic waves propagating through a plasma are
slightly different. Consider what happens when a linearly polarized electromagnetic wave, whose electric field is initially
of the form
propagates through the plasma.
We can represent a linearly polarized wave as a superposition of right- and left-hand circularly polarized waves of equal amplitudes. In other words,
where
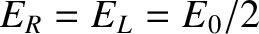 . Furthermore, in the high-frequency limit
. Furthermore, in the high-frequency limit
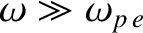 ,
,
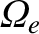 , Equations (9.72)
and (9.77) yield
where
, Equations (9.72)
and (9.77) yield
where
![$k_0 = (\omega/c)[1-(1/2)\,(\omega_{p\,e}/\omega)^2]$](img2683.png) , and
, and
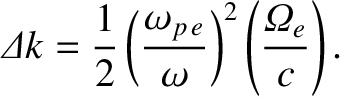 |
(9.85) |
Equations (9.81)–(9.84), in combination with some standard trigonometric identities (see Appendix B), give
It can be seen that the presence of the longitudinal magnetic field (whose strength is parameterized by
 ) causes the
plane of polarization of the wave to rotate as it propagates through the plasma. This effect is known as Faraday rotation.
Defining the angle of polarization,
) causes the
plane of polarization of the wave to rotate as it propagates through the plasma. This effect is known as Faraday rotation.
Defining the angle of polarization,
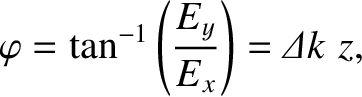 |
(9.88) |
the rate at which this angle advances as the wave propagates is
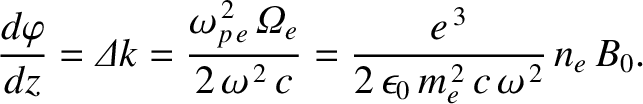 |
(9.89) |
Thus, a linearly polarized electromagnetic wave that propagates through a plasma with a slowly varying electron
number density, 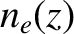 , and longitudinal magnetic field,
, and longitudinal magnetic field, 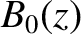 , has its plane of rotation rotated
through a net angle
, has its plane of rotation rotated
through a net angle
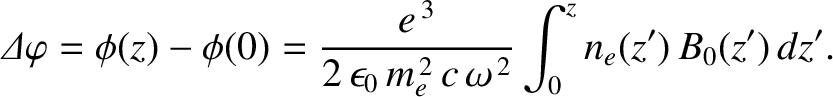 |
(9.90) |
Observe the very strong inverse depedence of
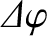 with the wave frequency,
with the wave frequency,  .
.
Pulsars are rapidly rotating neutron stars that emit regular blips of
highly polarized radio waves (Longair 2011). Hundreds of such objects have been found
in our galaxy since the first was discovered in 1967. By measuring
the variation of the angle of polarization, 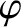 , of radio emission from a pulsar with frequency,
, of radio emission from a pulsar with frequency,  , astronomers can effectively determine
the line integral of
, astronomers can effectively determine
the line integral of 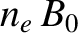 along the straight line joining the
pulsar to the Earth using formula (9.90) (ibid.). Here,
along the straight line joining the
pulsar to the Earth using formula (9.90) (ibid.). Here, 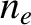 is the number
density of free electrons in the interstellar medium, whereas
is the number
density of free electrons in the interstellar medium, whereas  is the parallel (to the line joining the pulsar to the Earth) component of the galactic magnetic field. In order
to perform this calculation, astronomers must make the reasonable assumption that the
radiation was emitted by the pulsar with a common angle of polarization,
is the parallel (to the line joining the pulsar to the Earth) component of the galactic magnetic field. In order
to perform this calculation, astronomers must make the reasonable assumption that the
radiation was emitted by the pulsar with a common angle of polarization, 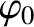 ,
over a wide range of different frequencies. By fitting Equation (9.90)
to the data, and then extrapolating to large
,
over a wide range of different frequencies. By fitting Equation (9.90)
to the data, and then extrapolating to large  , it is possible to
determine
, it is possible to
determine 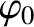 , and, hence, the amount,
, and, hence, the amount,
 ,
through which the polarization angle of the radiation has rotated, at a given frequency, during its passage to Earth.
,
through which the polarization angle of the radiation has rotated, at a given frequency, during its passage to Earth.
Astronomers can also determine the line integral of 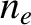 by looking at the variation of the arrival time of the various components of a pulsar radio blip with frequency (Longair 2011). This
calculation depends on the reasonable assumption that the components were emitted simultaneously, and then
traveled through interstellar space at the frequency dependent group velocity
by looking at the variation of the arrival time of the various components of a pulsar radio blip with frequency (Longair 2011). This
calculation depends on the reasonable assumption that the components were emitted simultaneously, and then
traveled through interstellar space at the frequency dependent group velocity
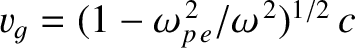 . [See Equation (9.34).] It follows that
the arrival time can be written
. [See Equation (9.34).] It follows that
the arrival time can be written
 |
(9.91) |
By fitting Equation (9.91)
to the data, and then extrapolating to large  , it is possible to
determine
, it is possible to
determine 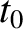 , and, hence,
, and, hence, 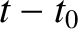 at a given frequency. Finally, once the line integrals of
at a given frequency. Finally, once the line integrals of 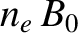 and
and
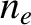 have been independently determined, estimates can be made of the mean electron number density, and the
mean galactic magnetic field, along the straight line joining the pulsar to the Earth.
have been independently determined, estimates can be made of the mean electron number density, and the
mean galactic magnetic field, along the straight line joining the pulsar to the Earth.
 -axis, through
a plasma with a longitudinal equilibrium magnetic field of strength,
-axis, through
a plasma with a longitudinal equilibrium magnetic field of strength,
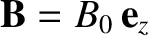 .
The equations of motion of an individual electron making up the plasma take the
form (see Appendix C)
where
.
The equations of motion of an individual electron making up the plasma take the
form (see Appendix C)
where 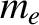 is the electron mass, and
is the electron mass, and 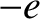 the electron charge.
Here,
the electron charge.
Here,  and
and  are the wave-induced displacements of the electron in the
are the wave-induced displacements of the electron in the  - and
- and  -directions, respectively.
(As before, it is a good approximation to neglect the wave-induced displacements of the ions, because of their relatively large mass.)
The former terms on the right-hand sides of the previous equations
represent the
-directions, respectively.
(As before, it is a good approximation to neglect the wave-induced displacements of the ions, because of their relatively large mass.)
The former terms on the right-hand sides of the previous equations
represent the  - and
- and  -directed forces exerted on the electron by the wave electric field,
-directed forces exerted on the electron by the wave electric field, 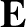 ,
whereas the latter terms represent the forces exerted by the equilibrium magnetic field when the electron moves (Fitzpatrick 2008).
(As before, we can neglect the forces due to the wave magnetic field, provided that the
electron motion remains non-relativistic.)
,
whereas the latter terms represent the forces exerted by the equilibrium magnetic field when the electron moves (Fitzpatrick 2008).
(As before, we can neglect the forces due to the wave magnetic field, provided that the
electron motion remains non-relativistic.)
 , whose electric field takes the form
, whose electric field takes the form
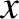
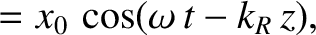
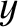
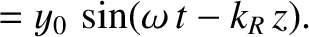

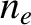 is the number density of electrons in the plasma then it follows that the
is the number density of electrons in the plasma then it follows that the  - and
- and  -components of the electric dipole moment per unit volume are
respectively. For the case of a circularly polarized wave, Equations (9.24) and (9.25) generalize to give (see Appendix C)
Thus, writing
-components of the electric dipole moment per unit volume are
respectively. For the case of a circularly polarized wave, Equations (9.24) and (9.25) generalize to give (see Appendix C)
Thus, writing 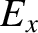 and
and  in the form (9.56) and (9.57), respectively,
the components of the magnetic intensity in the form
in the form (9.56) and (9.57), respectively,
the components of the magnetic intensity in the form
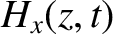
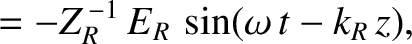
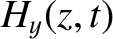
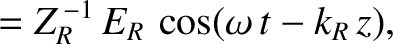
 and
and  in the form (9.63) and (9.64), respectively, Equations (9.65)–(9.68)
yield the nonlinear dispersion relation
in the form (9.63) and (9.64), respectively, Equations (9.65)–(9.68)
yield the nonlinear dispersion relation
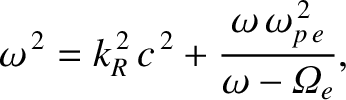
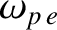 is the (electron) plasma frequency. [See Equation (9.28).] It follows that the refractive index of the plasma for right-hand circularly polarized waves is
whereas the effective impedance becomes
is the (electron) plasma frequency. [See Equation (9.28).] It follows that the refractive index of the plasma for right-hand circularly polarized waves is
whereas the effective impedance becomes
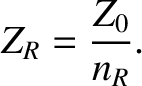
 is the impedance of free space.
is the impedance of free space.
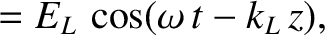
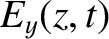
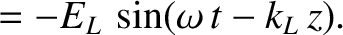
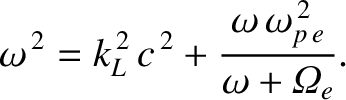
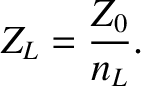
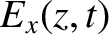
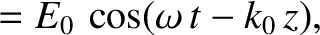
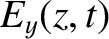
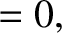
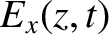
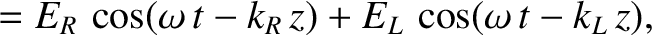
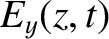
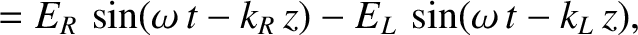
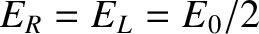 . Furthermore, in the high-frequency limit
. Furthermore, in the high-frequency limit
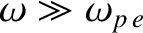 ,
,
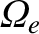 , Equations (9.72)
and (9.77) yield
, Equations (9.72)
and (9.77) yield
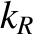
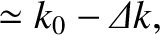
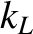
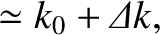
![$k_0 = (\omega/c)[1-(1/2)\,(\omega_{p\,e}/\omega)^2]$](img2683.png) , and
, and
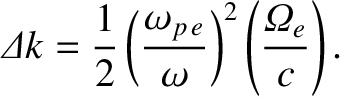
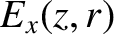
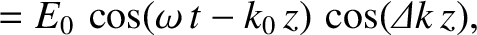


 ) causes the
plane of polarization of the wave to rotate as it propagates through the plasma. This effect is known as Faraday rotation.
Defining the angle of polarization,
) causes the
plane of polarization of the wave to rotate as it propagates through the plasma. This effect is known as Faraday rotation.
Defining the angle of polarization,
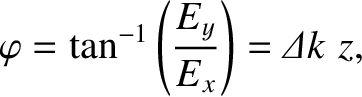
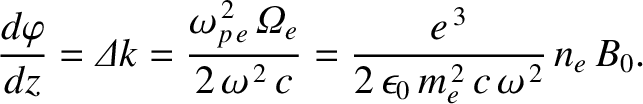
 , and longitudinal magnetic field,
, and longitudinal magnetic field,  , has its plane of rotation rotated
through a net angle
Observe the very strong inverse depedence of
, has its plane of rotation rotated
through a net angle
Observe the very strong inverse depedence of
 with the wave frequency,
with the wave frequency,  .
.
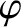 , of radio emission from a pulsar with frequency,
, of radio emission from a pulsar with frequency,  , astronomers can effectively determine
the line integral of
, astronomers can effectively determine
the line integral of 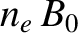 along the straight line joining the
pulsar to the Earth using formula (9.90) (ibid.). Here,
along the straight line joining the
pulsar to the Earth using formula (9.90) (ibid.). Here, 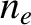 is the number
density of free electrons in the interstellar medium, whereas
is the number
density of free electrons in the interstellar medium, whereas  is the parallel (to the line joining the pulsar to the Earth) component of the galactic magnetic field. In order
to perform this calculation, astronomers must make the reasonable assumption that the
radiation was emitted by the pulsar with a common angle of polarization,
is the parallel (to the line joining the pulsar to the Earth) component of the galactic magnetic field. In order
to perform this calculation, astronomers must make the reasonable assumption that the
radiation was emitted by the pulsar with a common angle of polarization, 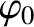 ,
over a wide range of different frequencies. By fitting Equation (9.90)
to the data, and then extrapolating to large
,
over a wide range of different frequencies. By fitting Equation (9.90)
to the data, and then extrapolating to large  , it is possible to
determine
, it is possible to
determine 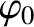 , and, hence, the amount,
, and, hence, the amount,
 ,
through which the polarization angle of the radiation has rotated, at a given frequency, during its passage to Earth.
,
through which the polarization angle of the radiation has rotated, at a given frequency, during its passage to Earth.
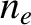 by looking at the variation of the arrival time of the various components of a pulsar radio blip with frequency (Longair 2011). This
calculation depends on the reasonable assumption that the components were emitted simultaneously, and then
traveled through interstellar space at the frequency dependent group velocity
by looking at the variation of the arrival time of the various components of a pulsar radio blip with frequency (Longair 2011). This
calculation depends on the reasonable assumption that the components were emitted simultaneously, and then
traveled through interstellar space at the frequency dependent group velocity
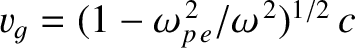 . [See Equation (9.34).] It follows that
the arrival time can be written
. [See Equation (9.34).] It follows that
the arrival time can be written
 , it is possible to
determine
, it is possible to
determine 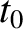 , and, hence,
, and, hence, 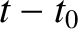 at a given frequency. Finally, once the line integrals of
at a given frequency. Finally, once the line integrals of 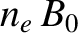 and
and
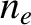 have been independently determined, estimates can be made of the mean electron number density, and the
mean galactic magnetic field, along the straight line joining the pulsar to the Earth.
have been independently determined, estimates can be made of the mean electron number density, and the
mean galactic magnetic field, along the straight line joining the pulsar to the Earth.