Polarization of Electromagnetic Waves
The electric component of an electromagnetic plane wave can oscillate in any direction normal to the
direction of wave propagation (which is parallel to the 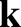 -vector) (Fitzpatrick 2008). Suppose that the wave is propagating in the
-vector) (Fitzpatrick 2008). Suppose that the wave is propagating in the 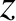 -direction. It follows that the electric field
can oscillate in any direction that lies in the
-direction. It follows that the electric field
can oscillate in any direction that lies in the  -
- plane. The actual direction of oscillation determines the polarization
of the wave. For instance, a vacuum electromagnetic wave of angular frequency
plane. The actual direction of oscillation determines the polarization
of the wave. For instance, a vacuum electromagnetic wave of angular frequency
 that is polarized in the
that is polarized in the  -direction has the associated electric field
-direction has the associated electric field
 |
(7.36) |
where
 . Likewise, a wave polarized in the
. Likewise, a wave polarized in the  -direction has the electric field
-direction has the electric field
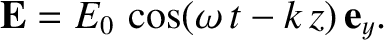 |
(7.37) |
These two waves are termed linearly polarized, because the electric field vector oscillates in a straight line.
However, other types of polarization are possible. For instance, if we combine two linearly polarized waves of equal amplitude, one polarized in the  -direction,
and one in the
-direction,
and one in the  -direction, that oscillate
-direction, that oscillate 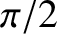 radians out of phase, then we obtain a circularly polarized wave:
radians out of phase, then we obtain a circularly polarized wave:
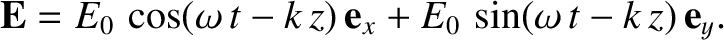 |
(7.38) |
This nomenclature arises from the fact that the tip of the electric field vector traces out a circle in the plane normal to the
direction of wave propagation.
To be more exact, the previous wave is a right-hand circularly polarized wave, because if the thumb of the right hand points in the direction of
wave propagation then the electric field vector rotates in the same sense as the fingers of this hand. Conversely, a left-hand
circularly polarized wave takes the form
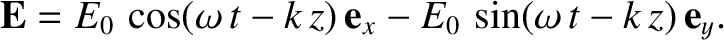 |
(7.39) |
Finally, if the  - and
- and  -components of the electric field in the previous two expressions have different (non-zero) amplitudes then
we obtain right-hand and left-hand elliptically polarized waves, respectively.
This nomenclature arises from the fact that the tip of the electric field vector traces out an ellipse in the plane normal to the
direction of wave propagation.
-components of the electric field in the previous two expressions have different (non-zero) amplitudes then
we obtain right-hand and left-hand elliptically polarized waves, respectively.
This nomenclature arises from the fact that the tip of the electric field vector traces out an ellipse in the plane normal to the
direction of wave propagation.
 -vector) (Fitzpatrick 2008). Suppose that the wave is propagating in the
-vector) (Fitzpatrick 2008). Suppose that the wave is propagating in the  -direction. It follows that the electric field
can oscillate in any direction that lies in the
-direction. It follows that the electric field
can oscillate in any direction that lies in the  -
- plane. The actual direction of oscillation determines the polarization
of the wave. For instance, a vacuum electromagnetic wave of angular frequency
plane. The actual direction of oscillation determines the polarization
of the wave. For instance, a vacuum electromagnetic wave of angular frequency
 that is polarized in the
that is polarized in the  -direction has the associated electric field
-direction has the associated electric field

 . Likewise, a wave polarized in the
. Likewise, a wave polarized in the  -direction has the electric field
-direction has the electric field
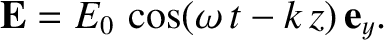
 -direction,
and one in the
-direction,
and one in the  -direction, that oscillate
-direction, that oscillate 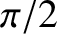 radians out of phase, then we obtain a circularly polarized wave:
radians out of phase, then we obtain a circularly polarized wave:
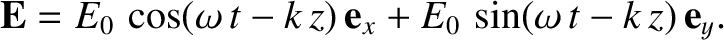
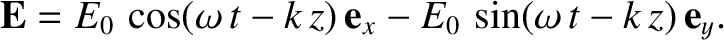
 - and
- and  -components of the electric field in the previous two expressions have different (non-zero) amplitudes then
we obtain right-hand and left-hand elliptically polarized waves, respectively.
This nomenclature arises from the fact that the tip of the electric field vector traces out an ellipse in the plane normal to the
direction of wave propagation.
-components of the electric field in the previous two expressions have different (non-zero) amplitudes then
we obtain right-hand and left-hand elliptically polarized waves, respectively.
This nomenclature arises from the fact that the tip of the electric field vector traces out an ellipse in the plane normal to the
direction of wave propagation.