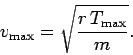Next: The conical pendulum
Up: Circular motion
Previous: Uniform circular motion
An object executing a circular orbit of radius  with uniform tangential
speed
with uniform tangential
speed  possesses a velocity vector
possesses a velocity vector 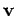 whose magnitude is constant, but
whose direction is continuously changing. It follows that the object must
be accelerating, since (vector) acceleration is the rate of change of (vector)
velocity, and the (vector) velocity is indeed varying in time.
whose magnitude is constant, but
whose direction is continuously changing. It follows that the object must
be accelerating, since (vector) acceleration is the rate of change of (vector)
velocity, and the (vector) velocity is indeed varying in time.
Figure 58:
Centripetal acceleration.
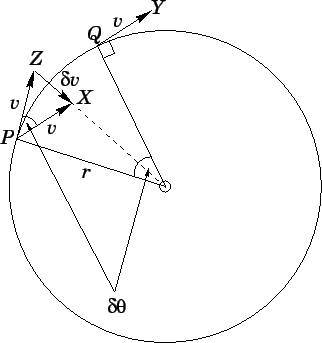 |
Suppose that the object moves from point 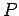 to point
to point  between times
between times  and
and 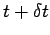 , as
shown in Fig. 58. Suppose, further, that the object rotates
through
, as
shown in Fig. 58. Suppose, further, that the object rotates
through 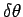 radians in this time interval. The vector
radians in this time interval. The vector
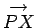 ,
shown in the diagram, is identical
to the vector
,
shown in the diagram, is identical
to the vector
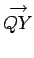 . Moreover, the angle subtended between vectors
. Moreover, the angle subtended between vectors
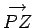 and
and
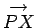 is simply
is simply 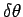 . The vector
. The vector
 represents
the change in vector velocity,
represents
the change in vector velocity, 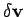 , between times
, between times  and
and 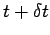 . It can be seen
that this vector is directed towards the centre of the circle. From standard trigonometry,
the length of vector
. It can be seen
that this vector is directed towards the centre of the circle. From standard trigonometry,
the length of vector
 is
is
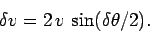 |
(256) |
However, for small angles
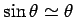 , provided that
, provided that  is measured in radians. Hence,
is measured in radians. Hence,
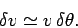 |
(257) |
It follows that
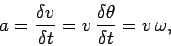 |
(258) |
where
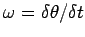 is the angular velocity of the object, measured
in radians per second.
In summary, an object executing a circular orbit, radius
is the angular velocity of the object, measured
in radians per second.
In summary, an object executing a circular orbit, radius  , with uniform tangential
velocity
, with uniform tangential
velocity  , and uniform angular velocity
, and uniform angular velocity 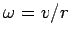 , possesses an acceleration
directed towards the centre of the circle--i.e., a centripetal acceleration--of
magnitude
, possesses an acceleration
directed towards the centre of the circle--i.e., a centripetal acceleration--of
magnitude
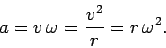 |
(259) |
Figure 59:
Weight on the end of a cable.
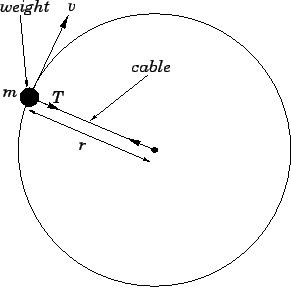 |
Suppose that a weight, of mass  , is attached to the end of a cable, of
length
, is attached to the end of a cable, of
length  , and whirled around such that the weight executes a horizontal circle,
radius
, and whirled around such that the weight executes a horizontal circle,
radius  , with uniform tangential velocity
, with uniform tangential velocity  . As we have just learned,
the weight is subject to a centripetal acceleration of magnitude
. As we have just learned,
the weight is subject to a centripetal acceleration of magnitude 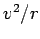 . Hence,
the weight experiences a centripetal force
. Hence,
the weight experiences a centripetal force
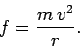 |
(260) |
What provides this force? Well, in the present example, the force is provided by the
tension 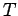 in the cable. Hence,
in the cable. Hence, 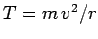 .
.
Suppose that the cable is such that it snaps whenever the tension in it
exceeds a certain critical value 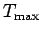 . It follows that there is a
maximum velocity with which the weight can be whirled around: namely,
. It follows that there is a
maximum velocity with which the weight can be whirled around: namely,
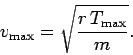 |
(261) |
If  exceeds
exceeds 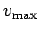 then the cable will break. As soon as the cable snaps,
the weight will cease to be subject to a centripetal force, so it will fly off--with
velocity
then the cable will break. As soon as the cable snaps,
the weight will cease to be subject to a centripetal force, so it will fly off--with
velocity 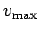 --along the straight-line
which is tangential to the circular orbit it was previously executing.
--along the straight-line
which is tangential to the circular orbit it was previously executing.



Next: The conical pendulum
Up: Circular motion
Previous: Uniform circular motion
Richard Fitzpatrick
2006-02-02

![]() to point
to point ![]() between times
between times ![]() and
and ![]() , as
shown in Fig. 58. Suppose, further, that the object rotates
through
, as
shown in Fig. 58. Suppose, further, that the object rotates
through ![]() radians in this time interval. The vector
radians in this time interval. The vector
![]() ,
shown in the diagram, is identical
to the vector
,
shown in the diagram, is identical
to the vector
![]() . Moreover, the angle subtended between vectors
. Moreover, the angle subtended between vectors
![]() and
and
![]() is simply
is simply ![]() . The vector
. The vector
![]() represents
the change in vector velocity,
represents
the change in vector velocity, ![]() , between times
, between times ![]() and
and ![]() . It can be seen
that this vector is directed towards the centre of the circle. From standard trigonometry,
the length of vector
. It can be seen
that this vector is directed towards the centre of the circle. From standard trigonometry,
the length of vector
![]() is
is
![]() , is attached to the end of a cable, of
length
, is attached to the end of a cable, of
length ![]() , and whirled around such that the weight executes a horizontal circle,
radius
, and whirled around such that the weight executes a horizontal circle,
radius ![]() , with uniform tangential velocity
, with uniform tangential velocity ![]() . As we have just learned,
the weight is subject to a centripetal acceleration of magnitude
. As we have just learned,
the weight is subject to a centripetal acceleration of magnitude ![]() . Hence,
the weight experiences a centripetal force
. Hence,
the weight experiences a centripetal force
![]() . It follows that there is a
maximum velocity with which the weight can be whirled around: namely,
. It follows that there is a
maximum velocity with which the weight can be whirled around: namely,